（本小题满分12分）在某次质量抽测后一数学老师随机抽取了30位（其中男、女各15名）同学的成绩，得出如下表，假设80分为“优秀”，否则为“不优秀”．
| 性别 |
成绩 |
| 男 |
83 81 96 68 83 77 86 97 78 64 85 91 90 99 82 |
| 女 |
74 70 68 86 92 72 76 78 78 64 86 66 79 68 70 |
（1）根据以上数据，试估计本次质量抽测数学科的优秀率（保留小数后三位）；
（2）完成下列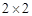
列联表：
| |
优秀 |
不优秀 |
合计 |
| 男 |
|
|
 |
| 女 |
|
|
|
| 合计 |
|
|
 |
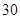（3）根据（2）中表格数据，利用独立性检验的方法判断，能否在犯错误的概率不超过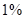
的前提下，认为“数学成绩”与“性别”有关？（其中
）
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
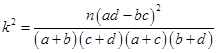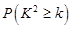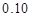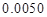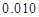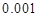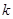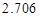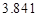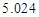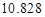均为正数，证明：
，并确定
（
为参数，
）上的点，点A的坐标为（1,0），
的长度均为
。
轴的正半轴为极轴建立极坐标系，求点M的极坐标；
的角平分线AD的延长线交它的外接圆于点E
，求
的大小。
.
时，讨论
的单调性；
时，若对任意
，存在
，使
，求实数
的取值范围.
的左焦点为F，过点F的直线与椭圆C相交于A，B两点，直线l的倾斜角为60o,
.
，求椭圆C的方程.