如图1,在Rt△ABC中,∠C=90°,D,E分别是AC,AB上的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
已知数列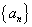 ,首项a 1 =3且2a n+1="S" n・S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n・S n-1 (n≥2).
(1)求证:{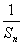 }是等差数列,并求公差;
}是等差数列,并求公差;
(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
已知集合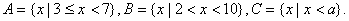
(1)求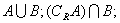
(2)若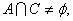 求a的取值范围.
求a的取值范围.
设函数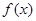
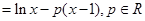
(1)求函数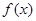 的单调区间
的单调区间
(2)设函数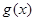 =
=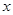
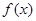
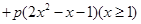 ,求证:当
,求证:当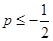 时,有
时,有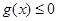 成立
成立
已知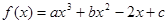 在
在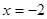 时有极大值6,在
时有极大值6,在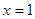 时有极小值
时有极小值
求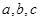 的值;并求
的值;并求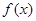 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.
已知曲线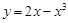 上一点
上一点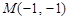 ,求:
,求:
(1)点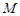 处的切线方程;
处的切线方程;
(2)点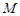 处的切线与
处的切线与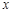 轴、
轴、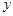 轴所围成的平面图形的面积。
轴所围成的平面图形的面积。