某山区的一种特产由于运输原因,长期只能在当地销售,当地政府对该特产的销售投资收益为:每投入x万元,可获得利润P=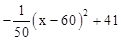 (万元)。当地政府拟规划加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。在外地销售的投资收益为:每投入
(万元)。当地政府拟规划加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投人100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出60万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售。在外地销售的投资收益为:每投入 万元,可获利润Q=
万元,可获利润Q=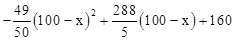 (万元)。
(万元)。
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O于D,AD的延长线交BC于E,若∠C = 25°,求∠A的度数.
解一元二次方程:(1)(x+1)2=3
(2)3y2+4y+1=0
化简二次根式:(1)

(2)
 (
( <0)
<0)
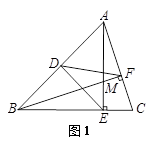
问题1已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=
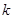 DF,则
DF,则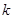 的值为____
的值为____ _.
_. 
拓展
问题2已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.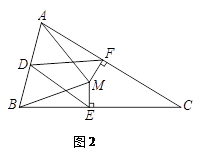
推广
问题3如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证 明你的结论.
明你的结论.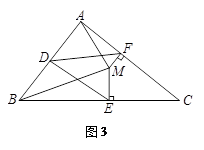
已知:如图1,平面直角坐标系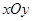 中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线
中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线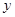 =-
=- +
+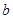 交折线O-A-B于点E.
交折线O-A-B于点E.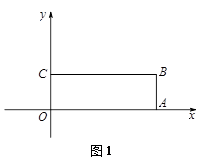
(1)在点D运动的过程中,若△ODE的面积为S,求S与
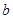 的函数关系式,
的函数关系式, 并写出自变量的取值范围;
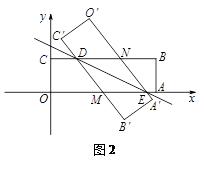
并写出自变量的取值范围;(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.探究四边形DMEN各边之间的数量关系,并对你的结论加以证明;
(3)问题(2)
 中的四边形DMEN中,ME的长为____________.
中的四边形DMEN中,ME的长为____________.