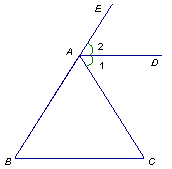
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长。
小萍同学灵活运用了轴对称知识,将图形进行翻折变换,巧妙地解答了此题。
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D、C点的对称点分别为E、F,延长EB、FC相交于G点,求证:四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值。
先化简,再求值: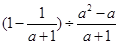 ,其中a=
,其中a= .
.
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则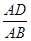 的值为.
的值为.
实验学校共有教师办公室22间,大的教师办公室每间可以安排10名教师在里面办公,小的教师办公室每间可以安排4名教师在里面办公.而实验学校一共有178名教师,这22间恰好能把实验学校的178名教师安排下,请你帮忙算一算,实验学校各有大小教师办公室多少间? (本题10分)
为了考察甲.乙两种小麦的长势,分别从中抽取10株麦苗,测得苗高如下(单位:cm):
甲: 12 13 14 13 10 16 13 13 15 11
乙: 6 9 7 12 11 16 14 16 20 19
(1)将数据整理,并通过计算后把下表填全:
| 小麦 |
中位数 |
众数 |
平均数 |
方差 |
| 甲 |
13 |
13 |
||
| 乙 |
16 |
21 |
(2)选择合适的数据代表,说明哪一种小麦长势较好
如图,已知∠B=∠C,AD∥BC,求证:AD平分∠CAE.