定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是_____,当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为______。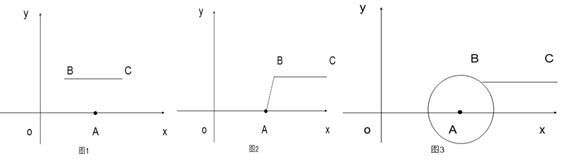
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A、M、H为顶点的三角形与△AOD相似,若存在,求出m的值;若不存在,请说明理由.
綦江县教委在推进课堂教学改革的过程中,为了切实减轻学生的课业负担,对义务教育阶段低年级学生原则上要求老师不布置课外作业,2015届九年级学生每天的课外作业总时间不得超过1小时(学生阅读、自学除外):
为了了解各校情况,县教委对其中40个学校2015届九年级学生课外完成作业时间调研后进行了统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题: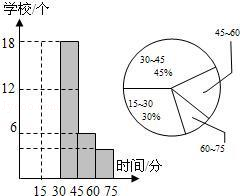
(1)计算出学生课外完成作业时间在30~45分钟的学校对应的扇形圆心角;
(2)将图中的条形图补充完整;
(3)计算出学生课外完成作业时间在60~75分钟的学校占调研学校总数的百分比.
如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.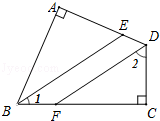
(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
解方程组和不等式组
(1)解方程组:
(2)解不等式组 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的 ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,在AB∥CD的前提下,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论.
(3)如图3,写出∠A+∠B+∠C+∠D+∠E+∠F的度数=__________.