平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,在AB∥CD的前提下,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论.
(3)如图3,写出∠A+∠B+∠C+∠D+∠E+∠F的度数=__________.
(第(1)题4分、第(2)题5分,共9分)(1) 计算:

 +
+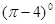
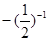 .
. (2)抛物线
 的部分图象如图所示,
的部分图象如图所示,
①求出函数解析式;
②写出与图象相关的2个正确结论:
(对称轴方程,图象与x正半轴、y轴交点坐标例外)
 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、 与
与 为对应角.
为对应角.
(1)如图1,若
 和
和 分别是以
分别是以 与
与 为顶角的等腰直角三角形,且两三角形旋转到使点
为顶角的等腰直角三角形,且两三角形旋转到使点 、
、 、
、 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段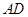 与线段
与线段 的关系;
的关系;(2)若
 和
和 为含有
为含有 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段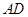 与线段
与线段 的关系,并说明理由;
的关系,并说明理由;(3)若
 和
和 为如图3的两个三角形,且
为如图3的两个三角形,且 =
= ,
,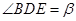 ,在绕点
,在绕点 旋转的过程中,直线
旋转的过程中,直线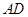 与
与 夹角的度数是否改变?若不改变,直接用含
夹角的度数是否改变?若不改变,直接用含 、
、 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由.
(本小题满分7分)
如图,已知抛物线y1=-x2+bx+c经过A(1,0),B(0,-2)两点,顶点为D.
(1)求抛物线y1 的解析式;
(2)将△AOB绕点A逆时针旋转90°后,得到△AO′ B′ ,将抛物线y1沿对称轴平移后经过点B′ ,写出平移后所得的抛物线y2 的解析式;
(3)设(2)的抛物线y2与
 轴的交点为B1,顶点为D1,若点M在抛物线y2上,且满足△MBB1的面积是△MDD1面积的2倍,求点M的坐标.
轴的交点为B1,顶点为D1,若点M在抛物线y2上,且满足△MBB1的面积是△MDD1面积的2倍,求点M的坐标.
(本题7分)对于二次函数 ,如果当
,如果当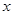 取任意整数时,
取任意整数时,
函数值 都是整数,此时称该点(
都是整数,此时称该点(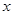 ,
, )为整点,该函数的图象为整点抛物线
)为整点,该函数的图象为整点抛物线
(例如: ).
).
(1)请你写出一个整点抛物线的解式.(不必证明);
(2)请直接写出整点抛物线
 与直线
与直线 围成的阴影图形中
围成的阴影图形中
(不包括边界)所含的整点个数.
(本题6分)已知:如图,△ABC是等边三角形,D是AB边上的点,将DB绕点D顺时针旋转60°得到线段DE,延长ED交AC于点F,连结DC、AE.
(1)求证:△ADE≌△DFC;
(2)过点E作EH∥DC交DB于点G,交BC于点H,连结AH.求∠AHE的度数;
(3)若BG=
 ,CH=2,求BC的长.
,CH=2,求BC的长.