已知，大正方形的边长为4，小正方形的边长为2，状态如图所示.大正方形固定不动，把小正方形以的速度向大正方形的内部沿直线平移，设平移的时间为秒，两个正方形重叠部分的面积为,完成下列问题：
(1)用含的式子表示，要求画出相应的图形，表明的范围；
(2)当，求重叠部分的面积；
(3)当，求的值.
如图，在矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD，BC于点E，F，垂足为点O．
（1）连接AF，CE，求证：四边形AFCE为菱形。
（2）求菱形AFCE的边长
如图，在△ABC中，MN∥BD交AC于点P，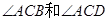 
的平分线分别交MN于点E，F。
（1）求证：PE=PF
（2）当MN与AC的交点P在什么位置时，四边形AECF是矩形，请说明理由；
（3）当△ABC满足什么条件时，四边形AECF是正方形（不需证明）
如图，直线AB与x轴交于点A（1，0），与y 轴交于点B（0，-2）。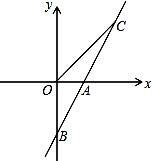
（1）求直线AB的解析式。
（2）若直线AB上的点C在第一象限，且S△BOC="2" ，求点C的坐标。
某商场服装部为了调动营业员的积极性，决定实行目标管理，即确定一个月销售目标，根据目标完成的情况对营业员进行适当的奖惩，为了确定一个适当的目标，商场统计了每个营业员在某月的销售额（万元）如下图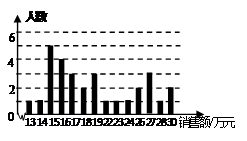
（1）求平均的月销售额及数据的中位数和众数
（2）如果想确定一个较高的销售目标，你认为月销售额定为多少合适？说明理由。
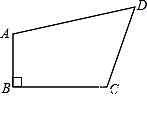
如图，在四边形ABCD中，AB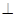
BC，AB=1，BC=2，CD=2，AD=3，求四边形ABCD的面积．