某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
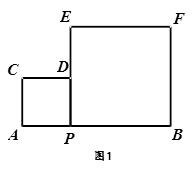
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC与正方形PBFE.
(1)在点P运动时,这两个正方形面积之和是定值吗?如果时求出;若不是,求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点A,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
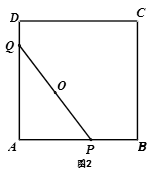
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向D点运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长。
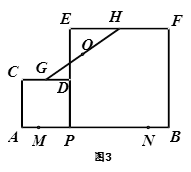
(4)如图(3),在“问题思考”中,若点M、N是线段AB上的两点,且AM=BM=1,点G、H分别是边CD、EF的中点.请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
已知:如图, 中,
中,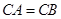 ,点
,点 为
为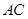 的中点,以
的中点,以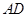 为直径的
为直径的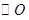 切
切 于点
于点 ,
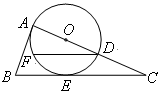
,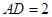 .
.
(1)求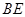 的长;(2)过点
的长;(2)过点 作
作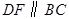 交
交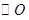 于点
于点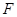 ,求
,求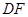 的长.
的长.
数学课上,年轻的刘老师在讲授“轴对称”时,设计了如下四种教学方法:
①教师讲,学生听;
②教师让学生自己做;
③教师引导学生画图,发现规律;
④教师让学生对折纸,观察发现规律,然后画图.
数学教研组长将上述教学方法作为调研内容发到全年级8个班420名同学手中,要求每位同学选出自己最喜欢的一种,他随机抽取了60名学生的调查问卷,统计如图: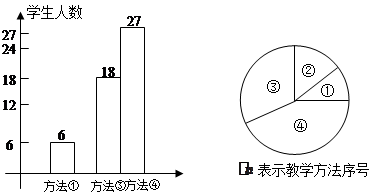
(1)请将条形统计图补充完整,并计算扇形统计图中方法③的圆心角.
(2)全年级同学中最喜欢的教学方法是哪一种?选择这种教学方法的约有多少人?
(3)假如抽取的60名学生集中在某两个班,这个调查结果还合理吗?为什么?
(4)请你对老师的教学方法提出一条合理化的建议.
如图,在四边形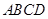 中,点
中,点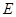 ,
,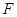 分别是
分别是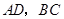 的中点,
的中点, 分别是
分别是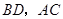 的中点,
的中点, 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?请证明你的结论.
是菱形?请证明你的结论.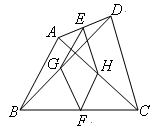
先化简,再求值: ,其中,
,其中,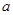 是方程
是方程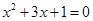 的根.
的根.
如图(1),我们将相同的两块含30°角的直角三角尺Rt△DEF与Rt△ABC叠合,使DE在AB上,DF过点C,已知AC=DE=6。将图(1)中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图(2)。
(1)求证:△CQD∽△APD
(2)连结PQ,设AP=x,求面积S△PCQ关于x的函数关系式;
(3)将图(1)中的△DEF 向左平移(A、D不重合),使边FD、FE分别交AC、BC于点M、N,如图(3),连结MN,试问△MCN面积是否存在最大值、如不存在,请说明理由;如存在请求出S△MCN 的最大值,