如图,在平面直角坐标系xOy中,抛物线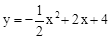 交y轴于点C,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转,与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
交y轴于点C,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转,与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。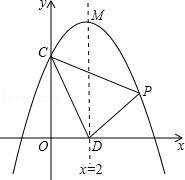
某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图:
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
解方程和不等式组:
(1) ;
;
(2) .
.
先化简,再求值: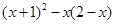 ,其中
,其中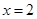 .
.
如图,在平面直角坐标系中,抛物线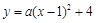 与
与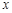 轴交于
轴交于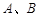 两点,与
两点,与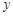 轴交于点
轴交于点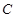 ,且点
,且点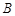 的坐标为
的坐标为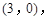 点
点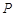 在这条抛物线上,且不与
在这条抛物线上,且不与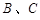 两点重合,过点
两点重合,过点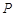 作
作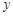 轴的垂线与射线
轴的垂线与射线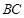 交于点
交于点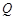 ,以
,以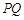 为边作
为边作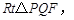 使
使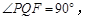 点
点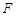 在点
在点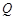 的下方,且
的下方,且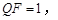 设线段
设线段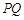 的长度为
的长度为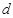 ,点
,点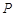 的横坐标为
的横坐标为 .
.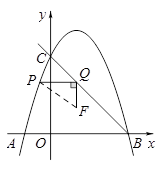
(1)求这条抛物线所对应的函数表达式;
(2)求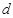 与
与 之间的函数关系式;
之间的函数关系式;
(3)当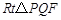 的边
的边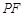 被
被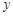 轴平分时,求
轴平分时,求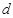 的值;
的值;
(4)以 为边作等腰直角三角形
为边作等腰直角三角形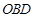 ,当
,当 时,直接写出点
时,直接写出点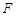 落在
落在 的边上时
的边上时 的值.
的值.
如图,在等边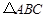 中,
中,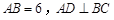 于点
于点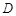 ,点
,点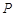 在边
在边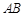 上运动,过点
上运动,过点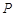 作
作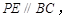 与边
与边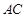 交于点
交于点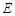 ,连结
,连结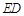 ,以
,以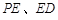 为邻边作□
为邻边作□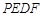 ,设□
,设□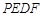 与
与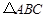 重叠部分图形的面积为
重叠部分图形的面积为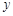 ,线段
,线段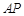 的长为
的长为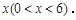
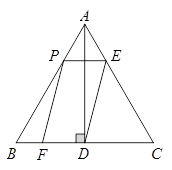
(1)求线段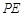 的长(用含
的长(用含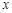 的代数式表示);
的代数式表示);
(2)当四边形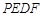 为菱形时,求
为菱形时,求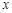 的值;
的值;
(3)求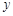 与
与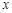 之间的函数关系式;
之间的函数关系式;
(4)设点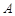 关于直线
关于直线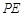 的对称点为点
的对称点为点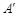 ,当线段
,当线段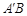 的垂直平分线与直线
的垂直平分线与直线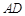 相交时,设其交点为
相交时,设其交点为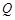 ,当点
,当点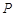 与点
与点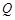 位于直线
位于直线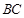 同侧(不包括点
同侧(不包括点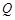 在直线
在直线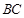 上)时,直接写出
上)时,直接写出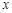 的取值范围.
的取值范围.