如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
计算:
如图所示,在平面直角坐标系中,抛物线 (
(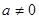 )经过
)经过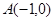 、
、 两点,抛物线与
两点,抛物线与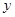 轴交点为
轴交点为 ,其顶点为
,其顶点为 ,连接
,连接 ,点
,点 是线段
是线段 上一个动点(不与
上一个动点(不与 、
、 重合),过点
重合),过点 作
作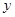 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接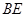 。
。
①求抛物线的解析式,并写出顶点 的坐标;
的坐标;
②如果 点的坐标为(
点的坐标为( ),
), 的面积为
的面积为 ,求
,求 与
与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围,并求出
的取值范围,并求出 的最大值;
的最大值;
③在②的条件上,当 取得最大值时,过点
取得最大值时,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,连接
,连接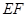 ,把
,把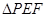 沿直线
沿直线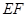 折叠,点
折叠,点 的对应点为
的对应点为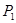 ,请直接写出
,请直接写出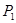 点坐标,并判断点
点坐标,并判断点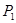 是否在该抛物线上;
是否在该抛物线上;
已知:如图,在正方形 中,
中, 是
是 上一点,延长
上一点,延长 到
到 ,使
,使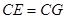 ,连接
,连接 并延长交
并延长交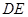 于
于 .
.
①求证: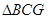 ≌
≌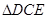 ;
;
②将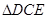 绕点
绕点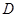 顺时针旋转
顺时针旋转 得到
得到 ,判断四边形
,判断四边形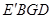 是什么特殊四边形?并说明理由.
是什么特殊四边形?并说明理由.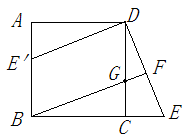
某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低 元。
元。
①填空:试用含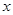 的代数式分别表示第二个月的销售价格和清仓时的销售量。(结果要化简)第二个月的销售价格为_____________元;清仓时的销售量为_____________件。
的代数式分别表示第二个月的销售价格和清仓时的销售量。(结果要化简)第二个月的销售价格为_____________元;清仓时的销售量为_____________件。
②如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
如图1,已知矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3;抛物线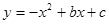 经过坐标原点O和x轴上另一点E(4,0)
经过坐标原点O和x轴上另一点E(4,0)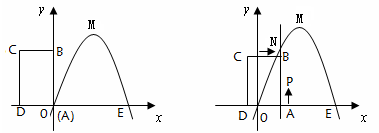
图1图2
(1)当x取何值时,该抛物线的最大值是多少?
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
① 当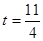 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
② 以P、N、C、D为顶点的多边形面积是否可能为5,若有可能,求出此时N点的坐标;若无可能,请说明理由.