如图1，已知直线y=kx与抛物线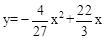
交于点A（3，6）．
（1）求直线y=kx的解析式和线段OA的长度；
（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；
（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？
先化简，再求值：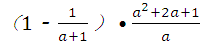
，其中a=
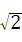﹣1．
为迎接2011年高中招生考试，某中学对全校九年级学生进行了一次数学摸底考试，并随机抽取了部分学生的测试成绩作为样本进行【解析】，绘制成了如下两幅不完整的统计图，请根据图中所给信息，【答案】下列问题：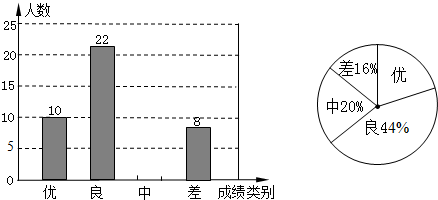
（1）请将表示成绩类别为“中”的条形统计图补充完整；
（2）在扇形统计图中，表示成绩类别为“优”的扇形所对应的圆心角是 72 度；
（3）学校九年级共有1000人参加了这次数学考试，估算该校九年级共有多少名学生的数学成绩可以达到优秀？
画△ABC，使其两边为已知线段a、b，夹角为β．（要求：用尺规作图，写出已知、求作；保留作图痕迹；不在已知的线、角上作图；不写作法）．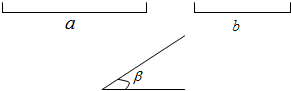
已知：
求作：
解分式方程：
．
（本小题8分）随着人们节能环保意识的增强，绿色交通工具越来越受到人们的青睐，电动摩托成为人们首选的交通工具，某商场计划用不超过
元购进
、
两种不同品牌的电动摩托
辆，预计这批电动摩托全部销售后可获得不少于
元的利润，、两种品牌电动摩托的进价和售价如下表所示：
设该商场计划进品牌电动摩托
辆，两种品牌电动摩托全部销售后可获利润
元.
写出与之间的函数关系式；
该商场购进品牌电动摩托多少辆时？获利最大，最大利润是多少？