如图，在平面坐标系中，直线y=﹣x+2与x轴，y轴分别交于点A，点B，动点P（a，b）在第一象限内，由点P向x轴，y轴所作的垂线PM，PN（垂足为M，N）分别与直线AB相交于点E，点F，当点P（a，b）运动时，矩形PMON的面积为定值2．当点E，F都在线段AB上时，由三条线段AE，EF，BF组成一个三角形，记此三角形的外接圆面积为S1，△OEF的面积为S2．试探究：
是否存在最大值？若存在，请求出该最大值；若不存在，请说明理由．
解不等式组
，并把解集在数轴上表示出来．
先化简，再求值：
，其中
．
如图，已知点D在双曲线
（
）的图象上，以D为圆心的⊙D与y轴相切于点C（0，4），与x轴交于A，B两点，抛物线
经过A，B，C三点，点P是抛物线上的动点，且线段AP与BC所在直线有交点Q．
（1）写出点D的坐标并求出抛物线的解析式；
（2）证明∠ACO=∠OBC；
（3）探究是否存在点P，使点Q为线段AP的四等分点？若存在，求出点P的坐标；若不存在，请说明理由．
如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D以每秒1个单位长度的速度由点A向点B匀速运动，到达B点即停止运动，M，N分别是AD，CD的中点，连接MN，设点D运动的时间为t．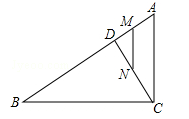
（1）判断MN与AC的位置关系；
（2）求点D由点A向点B匀速运动的过程中，线段MN所扫过区域的面积；
（3）若△DMN是等腰三角形，求t的值．
某公交公司有A，B型两种客车，它们的载客量和租金如下表：
红星中学根据实际情况，计划租用A，B型客车共5辆，同时送七年级师生到基地校参加社会实践活动，设租用A型客车x辆，根据要求回答下列问题：
（1）用含x的式子填写下表：
（2）若要保证租车费用不超过1900元，求x的最大值；
（3）在（2）的条件下，若七年级师生共有195人，写出所有可能的租车方案，并确定最省钱的租车方案．