阅读理解：对于任意正实数a、b，∵(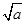
－
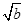)2≥0，∴a－2
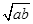＋b≥0，∴a＋b≥2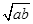，只有当a＝b时，等号成立.
结论：在a＋b≥2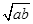（a、b均为正实数）中，若ab为定值p，则a+b≥2
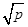，只有当a＝b时，a＋b有最小值2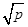. 根据上述内容，回答下列问题：
（1）若m＞0，只有当m＝ 时，m＋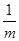
有最小值 ；
若m＞0，只有当m＝ 时，2m＋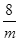
有最小值 .
（2）如图，已知直线L1：y＝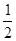
x＋1与x轴交于点A，过点A的另一直线L2与双曲线y＝
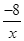（x>0）相交于点B（2，m），求直线L2的解析式.
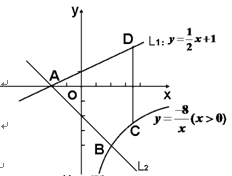
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.
如图，BD是⊙O的直径，过点D的切线交⊙O的弦BC的延长线于点E，弦AC∥DE交BD于点G
（1）求证：BD平分弦AC；
（2）若弦AD＝5㎝，AC＝8㎝，求⊙O的半径.
某商场开展购物抽奖活动，抽奖箱中有3个形状、大小和质地等完全相同的小球，分别标有数字1、2、3．顾客从中随机摸出一个小球，然后放回箱中，再随机摸出一个小球．
(1)利用树形图法或列表法(只选其中一种)，表示摸出小球可能出现的所有结果；
(2)若规定：两次摸出的小球的数字之积为9，则为一等奖；数字之积为偶数，则为二等奖．请你分别求出顾客抽中一等奖、二等奖的概率．
如图，在平面直角坐标系中，已知点
，
轴于A．将点B绕原点逆时针旋转90°后记作点
，作出旋转后的
.
（1）点的坐标为；
（2）求点B所经过的路径长.
已知关于x的方程
.
(1)当方程有两个不相等的实数根时,求k的取值范围;
(2)当方程的一个根是2时,求k的值.
计算：
．