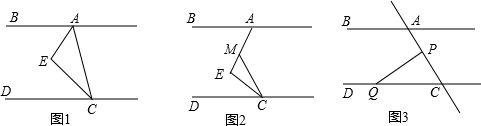阅读材料并回答问题：（本题8分）
我们知道，乘法公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，如：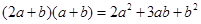
，就可以用图1或图2等图形的面积表示．
（1）请写出图3所表示的代数恒等式： ；
（2）试画一个几何图形，使它的面积表示：
；
（3）请仿照上述方法另写一个含有
，
的代数恒等式，并画出与它对应的几何图形．
如图，一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米，太阳光线与地面的夹角
∠ACD=60°.求接线柱AB的长.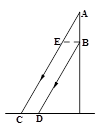
已知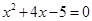
，求代数式
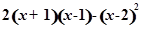的值．
解不等式组:
已知抛物线y=x2-4x+5，求出它的对称轴和顶点坐标.
(本题12分)如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°
（1）请判断AB与CD的位置关系并说明理由；
（2）如图2，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD否存在确定的数量关系？并说明理由；；
（3）如图3，P为线段AC上一定点，点Q为直线CD上一动点，①当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．②当点Q在射线CD的反向延长线上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？直接写出猜想结论，不需说明理由．