(本题12分)如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,①当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.②当点Q在射线CD的反向延长线上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?直接写出猜想结论,不需说明理由.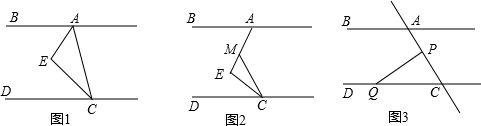
(1)计算:
(2)先化简,再求值: ,请代入一个你喜欢的值并进行计算.
,请代入一个你喜欢的值并进行计算.
(本小题满分11分)已知关于x的函数y=m -x-(m-1).
-x-(m-1).
(1)m=__________时,y=m -x-(m-1)是一次函数;
-x-(m-1)是一次函数;
(2)求证:对任何实数m,y=m -x-(m-1)的图像与
-x-(m-1)的图像与 都有公共点;
都有公共点;
(3)若是关于 的二次函数y=m
的二次函数y=m -x-(m-1)的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
-x-(m-1)的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
(4)是否存在这样的点P,使得对任何实数m,y=m -x-(m-1)的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
-x-(m-1)的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
(本小题满分9分)如图,在矩形ABCD中,E是CD边上一动点,设DE=x,作AF⊥AE交CB的延长线于点F.
(1)当点E不与点C,D重合时,求证:△ADE∽△ABF;
(2)连接EF,M为EF的中点,AB=4,AD=2, 当点E从D运动到C的过程中
①点M经过的路径是()
| A.直线 | B.线段 | C.射线 | D.圆弧 |
②求点M经过的路径的长;
③连接BM,直接写出BM的长度的最小值.
(本小题满分8分)某技工培训中心有钳工20名、车工30名. 现将这50名技工中的15人派往A地工作,35人派往B地工作,两地技工的工资情况如下表:
| 工种 属地 |
钳工 |
车工 |
 地 地 |
1800(元/月) |
1600(元/月) |
 地 地 |
1600(元/月) |
1200(元/月) |
设派往A地x名钳工时,这50名技工的月工资总额为y元.
(1)派往B地___________名钳工,派往B地___________名车工;
(2)求y关于x的函数关系式;
(3)若A地钳工的月工资总额不小于B地钳工的月工资总额,派往A地多少名钳工,可使这50名技工的月工资总额最高?
(本小题满分7分)如图,已知半径为2的⊙O与直线 相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线
相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线 的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4)
的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4)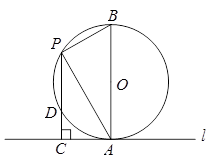
(1)当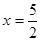 时,求弦PA、PB的长度;
时,求弦PA、PB的长度;
(2)当x为何值时,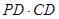 的值最大?最大值是多少?
的值最大?最大值是多少?