如图①所示,已知A、B为直线l上两点,点C为直线 上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)


如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P 320千米处.
(1) 说明本次台风会影响B市;(2)求这次台风影响B市的时间.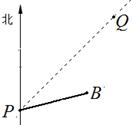
化简: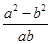 ÷(
÷(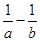 ).
).
计算: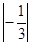 -(3.14-
-(3.14-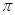 )0+(1-cos30°)×(
)0+(1-cos30°)×(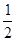 )-2
)-2
如图所示,已知在直角梯形 中,
中,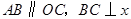 轴于点
轴于点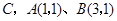 .动点
.动点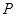 从
从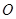 点出发,沿
点出发,沿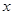 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过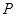 点作
点作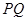 垂直于直线
垂直于直线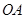 ,垂足为
,垂足为 .设
.设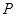 点移动的时间为
点移动的时间为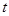 秒(
秒(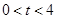 ),
), 与直角梯形
与直角梯形 重叠部分的面积为
重叠部分的面积为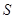 .
.
(1)求经过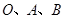 三点的抛物线解析式;
三点的抛物线解析式;
(2)求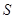 与
与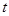 的函数关系式;
的函数关系式;
(3)将 绕着点
绕着点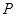 顺时针旋转
顺时针旋转 ,是否存在
,是否存在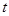 ,使得
,使得 的顶点
的顶点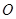 或
或 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出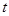 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
某电脑公司现有A,B,C三种型号的电脑和D,E两种型号的打印机.某校要从其中选购一台电脑和一台打印机送给山区小学.
(1) 写出所有选购方案(利用树状图或列表方法表示);
(2) 已知A、D是甲厂生产的产品,B、C、E是乙厂生产的产品.如果(1)中各种选购方案被选中的可能性相同,那么选中全套甲厂生产的产品的概率是多少?