国家规定“中小学生每天在校体育活动时间不低于1小时”，为此，某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生．根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：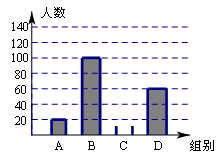
A组：t<0．5h； B组：0．5h≤t<1h；C组：1h≤t<1．5h； D组：t≥1．5h
请根据上述信息解答下列问题：
（1）C组的人数是 ，并补全直方图；
（2）本次调查数据的中位数落在 组内；
（3）若该辖区约有24 000名初中学生，请你估计其中达国家规定体育活动时间的人约有多少？
先化简代数式
，然后在取一组m,n的值代入求值
1 已知
的值
2 已知
，求
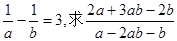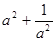的值
1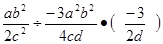 
2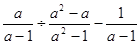
3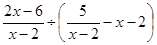
某公园有一个抛物线形状的观景拱桥ABC，其横截面如图所示，在图中建立的直角坐标系中，抛物线的解析式为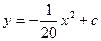
且过顶点C（0，5）（长度单位：m）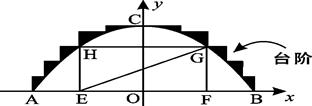
（1）直接写出c
的值；
（2）现因搞庆典活动，计
划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯，地毯的价格为20元 /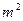 
,求购买地毯需多少元？
（3）在拱桥加固维修时，搭建的“脚手架”为矩形EFGH（H、G分别在抛物线的左右侧上），并铺设斜面EG.已知矩形EF
GH的周长为27.5 m，求斜面EG的倾斜角∠GEF的正切值.
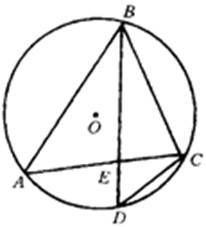
如图，△ABC内接于⊙O，D是弧AC的中点，求证：CD2=DE?DB。