(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5, 5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .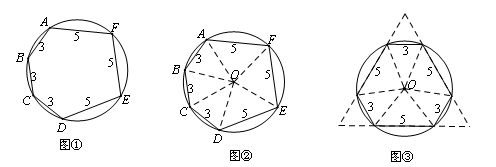
(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.
请你仿照小森的思考方式,求出这个八边形的面积.
如图①所示,直线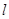 :
: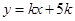 与
与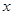 轴负半轴、
轴负半轴、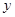 轴正半轴分别交于
轴正半轴分别交于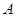 、
、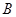 两点.
两点.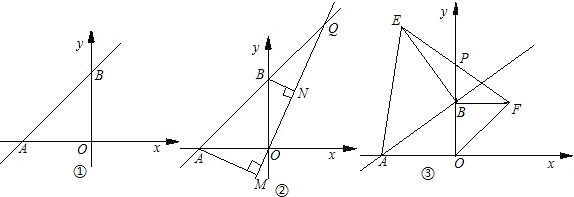
(1)当 时,试确定直线
时,试确定直线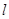 的解析式;
的解析式;
(2)在(1)的条件下,如图②所示,设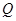 为
为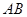 延长线上一点,连接
延长线上一点,连接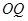 ,过
,过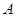 、
、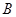 两点分别作
两点分别作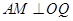 于
于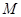 ,
, 于
于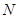 ,若
,若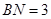 ,
,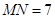 ,求
,求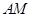 的长;
的长;
(3)当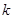 取不同的值时,点
取不同的值时,点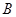 在
在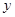 轴正半轴上运动,分别以
轴正半轴上运动,分别以 、
、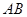 为边在第一、第二象限作等腰直角
为边在第一、第二象限作等腰直角 和等腰直角
和等腰直角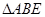 ,连
,连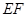 交
交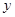 轴于
轴于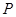 点,问当点
点,问当点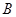 在
在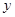 轴上运动时,试猜想
轴上运动时,试猜想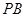 的长是否为定值,若是,请求出其值;若不是,请说明理由.
的长是否为定值,若是,请求出其值;若不是,请说明理由.
如图,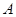 城气象台测得台风中心在
城气象台测得台风中心在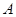 城的正西方
城的正西方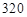 千米的
千米的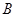 处,以每小时
处,以每小时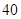 千米的速度向北偏东
千米的速度向北偏东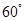 的
的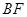 方向移动,距台风中心
方向移动,距台风中心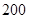 千米的范围内是受这次台风影响的区域.问
千米的范围内是受这次台风影响的区域.问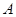 城是否会受到这次台风的影响?为什么?如果会受到影响,求出
城是否会受到这次台风的影响?为什么?如果会受到影响,求出 城遭受这次台风影响持续的时间.
城遭受这次台风影响持续的时间.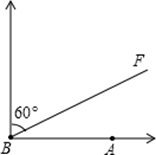
一张边长为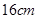 正方形的纸片,剪去两个面积一定且一样的小长方形得到一个“
正方形的纸片,剪去两个面积一定且一样的小长方形得到一个“ ”图案如图1所示.小长方形的的相邻两边长
”图案如图1所示.小长方形的的相邻两边长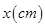 与
与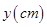 之间的函数关系如图2所示:
之间的函数关系如图2所示: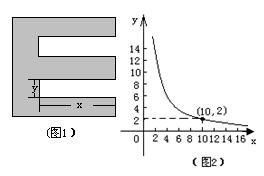
(1)求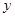 与
与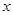 之间的函数关系式;
之间的函数关系式;
(2)“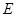 ”图案的面积是多少?
”图案的面积是多少?
(3)如果小长方形中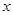 满足
满足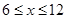 ,
,
求其相邻边长的范围.
某市为治理污水,需要铺设一段全长为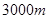 的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加
的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加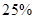 ,结果提前
,结果提前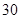 天完成这一任务,实际每天铺设多长管道?
天完成这一任务,实际每天铺设多长管道?
如图,在直角坐标系中,点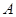 是反比例函数
是反比例函数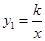 的图象上一点,
的图象上一点, 轴的正半轴于
轴的正半轴于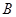 点,
点,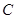 是
是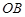 的中点;一次函数
的中点;一次函数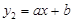 的图象经过
的图象经过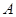 、
、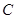 两点,并交
两点,并交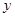 轴于点
轴于点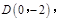 若
若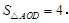
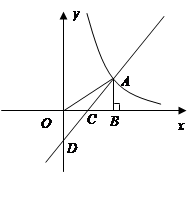
(1)求反比例函数和一次函数的解析式;
(2)观察图象,请写出在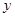 轴的右侧,当
轴的右侧,当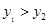 时,
时,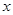 的取值范围.
的取值范围.