如图，在平面直角坐标系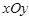
中，二次函数
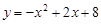的图象与一次函数
的图象交于A、B两点，点A在x轴上，点B的纵坐标为
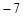．点P是二次函数图象上A、B两点之间的一个动点（不与点A、B重合），设点P的横坐标为m，过点P作x轴的垂线交AB于点C，作PD⊥AB于点D．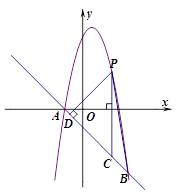
（1）求b及sin∠ACP的值；
（2）用含m的代数式表示线段PD的长；
（3）连接PB，线段PC把△PDB分成两个三角形，是否存在适合的m值，使这两个三角形的面积之比为
．如果存在，直接写出m的值；如果不存在，请说明理由．
如图，以O为圆心的弧
度数为60 o，∠BOE＝45o，DA⊥OB，EB⊥OB．
（1）求
的值；
（2）若OE与交于点M，OC平分∠BOE，连接CM．说明：CM为⊙O的切线；
（3）在（2）的条件下，若BC＝1，求tan∠BCO的值．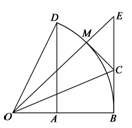
已知二次函数y＝x2＋2ax－2．
（1）求证：经过点（0，
）且与x轴平行的直线与该函数的图象总有两个公共点；
（2）该函数和y＝－
x2＋(a－3)x+
的图象都经过x轴上两个不同的点A、B，求a的值．
桌面上有5张背面相同的卡片，正面分别写着数字“1”、“2”、“3”、“4”、 “5”．将卡片背面朝上洗匀．
（1）小军从中任意抽取一张，抽到偶数的概率是；
（2）小红从中同时抽取两张．规定：抽到的两张卡片上的数字之和为奇数，则小军胜，否则小红胜．你认为这个游戏公平吗？请用树状图或表格说明你的理由．
南京市为了构建立体的道路网络，大力发展江北经济，决定修建一条六合到主城的轻轨铁路．为了使工程提前3个月完成，需将原定的工作效率提高10％．原计划完成这项工程需要多少个月？
下列为某校初三参加的“迎青奥”知识能力竞赛的25位同学的成绩：
78，86，98，90，95， 88，94，80，89，77， 87，73，65，84，87，
96，84，74，98，86， 83，67，88，68，85．
（1）完成下表：
（2）补全频数分布直方图；
（3）若超过均分的将获奖，请计算本次竞赛获奖的比例．