如图1，已知直线y=2x+2与y轴、x轴分别交于A、B两点，以B为直角顶点在第二象限作等腰Rt△ABC
（1）求点C的坐标，并求出直线AC的关系式．
（2）如图2，直线CB交y轴于E，在直线CB上取一点D，连接AD，若AD=AC，求证：BE=DE．
（3）如图3，在（1）的条件下，直线AC交x轴于M，P（−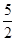
，k）是线段BC上一点，在线段BM上是否存在一点N，使直线PN平分△BCM的面积？若存在，请求出点N的坐标；若不存在，请说明理由．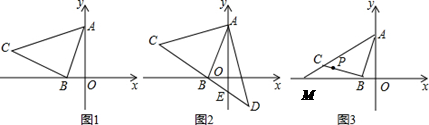
如图，A点在B处的北偏东40°方向，C点在B处的北偏东85°方向，A点在C处的北偏西45°方向，求∠BAC及∠BCA的度数.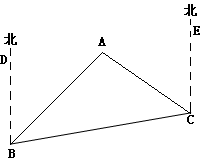 
如图，已知∠1+∠2=180°，∠B=∠3，你能判断∠C与∠AED的大小关系吗？并说明理由.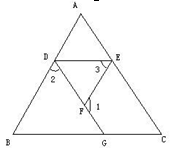
已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数.
（本小题满分8分）
四边形ABCD中，∠A =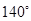
，∠D =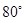
．
（1）如图1，若∠B=∠C，试求出∠C的度数；
（2）如图2，若∠ABC的角平分线BE交DC于点E，且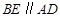
，试求出∠C的度数；
（3）如图3，若∠ABC和∠BCD的角平分线交于点E，试求出∠BEC的度数．
（本小题满分10分）
如图，长方形OABC中，O为平面直角坐标系的原点，点A、C的坐标分别为A（3，0）、
C（0，2），点B在第一象限。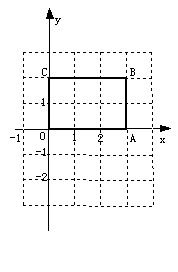
(1)写出点B的坐标；
(2)若过点C的直线交长方形的OA边于点D，且把长方形OABC的周长分成2∶3的两部分，求点D的坐标；
(3)如果将（2）中的线段CD向下平移3个单位长度，得到对应线段C′D′，在平面直角坐标系中画出△CD′C′，并求出它的面积。