如图①，一条笔直的公路上有A、B、C三地，B．C两地相距150千米，甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B两地．甲、乙两车到A地的距离y1、y2（千米）与行驶时间x（时）的关系如图②所示．根据图像进行以下探究：
（1）请在图①中标出A地的位置，并作简要的文字说明；
（2）求图②中M点的坐标，并解释该点的实际意义；
（3）在图②中补全甲车的函数图像，求甲车到A地的距离y1与行驶时间x的函数表达式；
（4）A地设有指挥中心，指挥中心及两车都配有对讲机，两部对讲机在15千米之内（含15千米）时能够互相通话，求两车可以同时与指挥中心用对讲机通话的时间．
如图，小岛A在港口P的南偏西45°方向，距离港口81海里处．甲船从A出发，沿AP方向以9海里/时的速度驶向港口，乙船从港口P出发，沿南偏东60°方向，以18海里/时的速度驶离港口，现两船同时出发．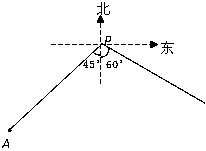
（1）出发后几小时两船与港口P的距离相等；
（2）出发后几小时乙船在甲船的正东方向？（结果精确到0．1小时）（参考数据：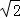
≈1．41，
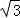≈1．73）
如图，某一时刻太阳光从教室窗户射入室内，与地面的夹角∠BPC为30°，窗户的一部分在教室地面所形成的影长PE为3．5米，窗户的高度AF为2．5米．求窗外遮阳蓬外端一点D到教室窗户上椽的距离AD．（结果精确0．1米）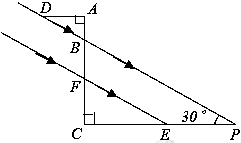
如图，在矩形ABCD中，AB=2AD，线段EF=10．在EF上取一点M，分别以EM、MF为一边作矩形EMNH、矩形MFGN，使矩形MFGN∽矩形ABCD．令MN=x，当x为何值时，矩形EMNH的面积S有最大值，最大值是多少？
如图，光源L距地面（LN）8米，距正方体大箱顶站（LM）2米，已知，在光源照射下，箱子在左侧的影子BE长5米，求箱子在右侧的影子CF的长．（箱子边长为6米）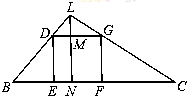
如图，三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小都相同．正常水位时，大孔水面宽度AB=20米，顶点M距水面6米（即MO=6米），小孔顶点N距水面4．5米（即NC=4．5米）．当水位上涨刚好淹没小孔时，借助图中的直角坐标系，求此时大孔的水面宽度EF．