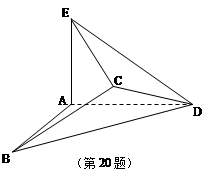(本小题满分16分)
对于函数 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数 和
和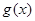 在点P处相切,称点P为这两个函数的切点.设函数
在点P处相切,称点P为这两个函数的切点.设函数 ,
, .
.
(1)当 ,
, 时,判断函数
时,判断函数 和
和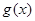 是否相切?并说明理由;
是否相切?并说明理由;
(2)已知 ,
, ,且函数
,且函数 和
和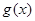 相切,求切点P的坐标;
相切,求切点P的坐标;
(3)设 ,点P的坐标为
,点P的坐标为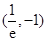 ,问是否存在符合条件的函数
,问是否存在符合条件的函数 和
和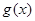 ,使得它们在点P处相切?若点P的坐标为
,使得它们在点P处相切?若点P的坐标为 呢?(结论不要求证明)
呢?(结论不要求证明)
等差数列 不是常数列,且
不是常数列,且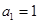 ,若
,若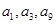 构成等比数列.
构成等比数列.
(1)求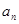 ;
;
(2)求数列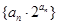 前n项和
前n项和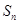
求函数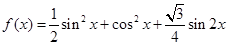 .
.
(1)求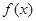 的周期与值域;
的周期与值域;
(2)求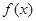 在
在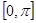 上的单调递减区间.
上的单调递减区间.
设函数 f (x)=ax-lnx-3(a∈R),g(x)=xe1-x.
(Ⅰ)若函数 g(x) 的图象在点 (0,0) 处的切线也恰为 f (x) 图象的一条切线,求实数a的值;
(Ⅱ)是否存在实数a,对任意的 x∈(0,e],都有唯一的 x0∈[e-4,e],使得 f (x0)=g(x) 成立.若存在,求出a的取值范围;若不存在,请说明理由.
注:e是自然对数的底数.
已知椭圆C: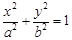 (a>0,b>0)的离心率为
(a>0,b>0)的离心率为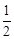 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+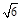 =0相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E.
=0相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:直线AE与x轴相交于定点Q;
(III)求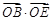 的取值范围.
的取值范围.
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
(Ⅰ)若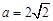 ,求证:AB//平面CDE;
,求证:AB//平面CDE;
(Ⅱ)求实数a的值,使得二面角A-EC-D的大小为60°.