(1)已知点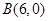 和
和 ,过点
,过点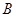 的直线
的直线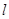 与过点
与过点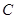 的直线
的直线 相交于点
相交于点 ,设直线
,设直线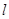 的斜率为
的斜率为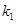 ,直线
,直线 的斜率为
的斜率为 ,如果
,如果 ,求点
,求点 的轨迹;
的轨迹;
(2)用正弦定理证明三角形外角平分线定理:如果在 中,
中, 的外角平分线
的外角平分线 与边
与边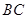 的延长线相交于点
的延长线相交于点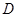 ,则
,则 .
.
(1)(满分7分) 选修4一2:矩阵与变换
二阶矩阵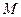 对应的变换将点
对应的变换将点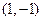 与
与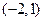 分别变换成点
分别变换成点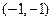 与
与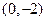 .
.
(Ⅰ)求矩阵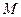 ;
;
(Ⅱ)设直线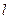 在矩阵
在矩阵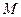 对应变换的作用下得到直线
对应变换的作用下得到直线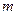 :
: 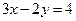 ,求
,求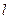 的方程.
的方程.
设椭圆M: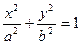 (a>b>0)的离心率为
(a>b>0)的离心率为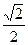 ,长轴长为
,长轴长为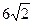 ,设过右焦点F倾斜角
,设过右焦点F倾斜角
为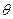 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(Ⅱ)求证| AB | =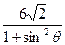 ;
;
(Ⅲ)设过右焦点F且与直线AB垂直的直线交椭圆M于C, D,求|AB| + |CD|的最小值。
D,求|AB| + |CD|的最小值。
已知定点F(1,0),动点P在y轴上运动,过点P作PM交x轴于点M,并延长MP到点N,且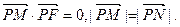
(Ⅰ)求动点N的轨迹方程;
(Ⅱ)直线l与动点N的轨迹交于A、B两点,若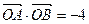 ,且
,且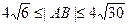 ,
,
求直线l的斜率k的取值范围.
双曲线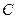 的中心在原点,右焦点为
的中心在原点,右焦点为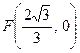 ,渐近线方程为
,渐近线方程为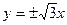 .
.
(Ⅰ)求双曲线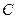 的方程;
的方程;
(Ⅱ)设直线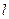 :
: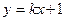 与双曲线
与双曲线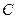 交于
交于 、
、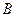 两点,问:当
两点,问:当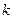 为何值时,以
为何值时,以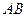 为直径的圆过原点。
为直径的圆过原点。
若圆C经过点 和
和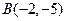 ,且圆心C在直线
,且圆心C在直线 上,求圆C的方程.
上,求圆C的方程.