已知数列 是等差数列,
是等差数列, 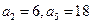 ;数列
;数列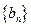 的前n项和是
的前n项和是 ,且
,且 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 求证:数列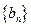 是等比数列;
是等比数列;
(3) 记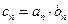 ,求
,求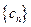 的前n项和
的前n项和 .
.
(满分10分) 在锐角 中,
中,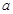 ,
, ,
, 分别为内角
分别为内角 ,
,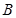 ,
, 所对的边,且满足
所对的边,且满足
(Ⅰ)求角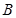 的大小;
的大小;
(Ⅱ)若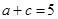 ,且
,且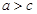 ,
, ,求
,求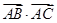 的值.
的值.
一次考试中,五名学生的数学、物理成绩如下表所示:
| 学生 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 数学(x分) |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)请在所给的直角坐标系中画出它们的散点图
(2)并求这些数据的线性回归方程 =bx+a.
=bx+a.
附:线性回归方程 中,
中,
其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
某单位2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
| 人数 |
管理 |
技术开发 |
营销 |
生产 |
共计 |
| 老年 |
40 |
40 |
40 |
80 |
200 |
| 中年 |
80 |
120 |
160 |
240 |
600 |
| 青年 |
40 |
160 |
280 |
720 |
1 200 |
| 小计 |
160 |
320 |
480 |
1 040 |
2 000 |
(1)若要抽取40人调查身体状况,则应怎样抽样?
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
(3)若要抽20人调查对北京9月3日阅兵情况的了解,则应怎样抽样?
如图是某市有关部门根据该市干部的月收入情况,画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息解答下列问题.
(1)求样本中月收入在[2 500,3 500)的人数;
(2)为了分析干部的收入与年龄、职业等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽多少人?
(3)试估计样本数据的中位数.