如图是某市有关部门根据该市干部的月收入情况,画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息解答下列问题.
(1)求样本中月收入在[2 500,3 500)的人数;
(2)为了分析干部的收入与年龄、职业等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽多少人?
(3)试估计样本数据的中位数.
已知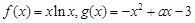 .
.
(1)已知函数h(x)=g(x)+ax3的一个极值点为1,求a的取值;
(2) 求函数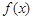 在
在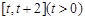 上的最小值;
上的最小值;
(3)对一切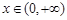 ,
,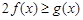 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知函数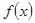 是定义在
是定义在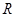 上的偶函数,且当
上的偶函数,且当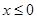 时,
时,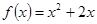 .现已画出函数
.现已画出函数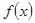 在
在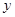 轴左侧的图像,如图所示,并根据图像
轴左侧的图像,如图所示,并根据图像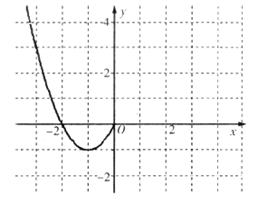
(1)写出函数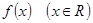 的增区间;
的增区间;
(2)写出函数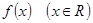 的解析式;
的解析式;
(3)若函数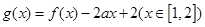 ,求函数
,求函数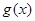 的最小值。
的最小值。
已知函数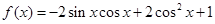
(1)设方程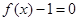 在(0,
在(0,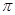 )内有两个零点
)内有两个零点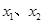 ,求
,求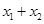 的值;
的值;
(2)若把函数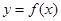 的图像向左移动
的图像向左移动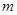
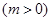 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于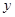 轴对称,求
轴对称,求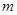 的最小值。
的最小值。
鑫隆房地产公司用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为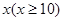 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为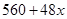 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
在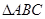 中,设内角
中,设内角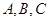 的对边分别为
的对边分别为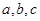 向量
向量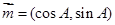 ,向量
,向量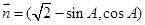 ,若
,若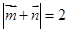
(1)求角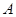 的大小;
的大小;
(2)若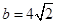 ,且
,且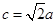 ,求
,求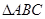 的面积.
的面积.