(本题满分10分)
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: .
.
(1)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在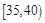 岁的人数;
岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人,记这3名志愿者中“年龄低于35岁”的人数为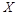 ,求
,求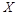 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)
已知向量m ,n
,n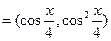 ,函数
,函数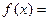 m·n.
m·n.
(1)若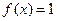 ,求
,求 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是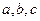 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分15分)
已知函数
(1)求 的单调区间;
的单调区间;
(2)若 ,
, ,求
,求 的取值范围.
的取值范围.
(本小题满 分15分)
分15分)
已 知椭圆
知椭圆 的离心率
的离心率 ,过点
,过点
 和
和
 的直线与原点的距离为
的直线与原点的距离为 .
.
(1)求椭圆的方程;
(2)设 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过 作直线交椭圆于
作直线交椭圆于
 、
、 两点,求
两点,求 的内切圆半径
的内切圆半径 的最大值.
的最大值.
(本小题满分14分)
如图(1)已知矩形 中,
中, ,
, 、
、 分别是
分别是 、
、 的中点,点
的中点,点 在
在 上,且
上,且 ,把
,把 沿着
沿着 翻折,使点
翻折,使点 在平面
在平面 上的射影恰为点
上的射影恰为点 (如图(2))。
(如图(2))。
(1)求证:平面

 平面
平面 ;
;
(2)求二面角 的大小.
的大小.

图(1)图(2)
(本小题满分14分)
桌面上有三颗均匀的骰子(6个面上分别标有数字1,2,3,4,5,6)。重复下面的操作,直到桌 面上没有骰子:将骰子全部抛掷,然后去掉那些朝上点数为奇数的骰子。记操作三次之内(含三次)去掉的骰子的颗数为X.
面上没有骰子:将骰子全部抛掷,然后去掉那些朝上点数为奇数的骰子。记操作三次之内(含三次)去掉的骰子的颗数为X.
(1)求 ;
;
(2)求X的分布列及期望 .
.