如图，□ABCD中，AB⊥AC，AB＝1，BC＝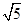
．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．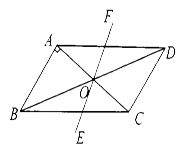
(1)试说明在旋转过程中，线段AF与EC总保持相等；
(2)在旋转过程中，四边形BEDF可能是菱形吗?如果不能，请说明理由；如果能，请直接写出此时AC绕点O顺时针旋转的度数．
分解因式4a2bc－3a2c2＋8abc－6ac2；
分解因式（m2＋3m）2－8（m2＋3m）－20；
计算（1）(2x+y-3)(2x-y+3)（2）
如图1，小明将一张矩形纸片沿对角线剪开，得到两张全等直角三角形纸片（如图2），量得他们的斜边长为10cm，较小锐角为30°，再将这两张三角纸片摆成如图3的形状，使点B、F、D在同一条直线上，F为公共直角顶点.
小明在对这两张三角形纸片进行如下操作时遇到了两个问题，请你帮助解决。（1）将图3中的△ABF绕点F顺时针方向旋转30°到图4的位置，A1F交DE于点G，请你求出线段EG的长度；（2）将图3中的△ABF沿直线AF翻折到图5的位置，AB1交DE于点H，请证明：AH=DH.
△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点，就下面给出的三种情况，如图8中的①②③，先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度．并利用图③证明你的结论．