如图,在△ABC中,AB=AC,AD是△ABC的角平分线,作AE∥BC,CE∥AD,AE、CE交于点E.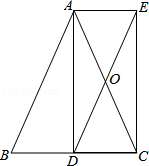
(1)证明:四边形ADCE是矩形.
(2)若DE交AC于点O,证明:OD∥AB且OD=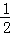 AB.
AB.
已知关于 的一元二次方程 .
(1)求证:方程有两个不相等的实数根.
(2)如果方程的两实数根为 , ,且 ,求 的值.
“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
|
成绩 分 |
7 |
8 |
9 |
10 |
|
人数 人 |
2 |
5 |
4 |
4 |
(1)这组数据的众数是 ,中位数是 .
(2)已知获得10分的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
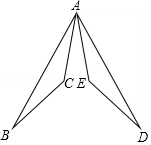
如图,已知 , , .
求证: .
如图,已知抛物线 过点 , 和点 , .过点 作直线 轴,交 轴于点 .
(1)求抛物线的解析式;
(2)在抛物线上取一点 ,过点 作直线 的垂线,垂足为 .连接 ,使得以 , , 为顶点的三角形与 相似,求出对应点 的坐标;
(3)抛物线上是否存在点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.

如图,已知 的顶点坐标分别为 , , .动点 , 同时从 点出发, 沿 , 沿折线 ,均以每秒1个单位长度的速度移动,当一个动点到达终点 时,另一个动点也随之停止移动,移动的时间记为 秒.连接 .
(1)求直线 的解析式;
(2)移动过程中,将 沿直线 翻折,点 恰好落在 边上点 处,求此时 值及点 的坐标;
(3)当点 , 移动时,记 在直线 右侧部分的面积为 ,求 关于时间 的函数关系式.
