在北京,乘坐地铁是市民出行时经常采用的一种交通方式.据调查,新票价改革政策的实施给北京市轨道交通客流带来很大变化.根据2015年1月公布的调价后市民当时乘坐地铁的相关调查数据,制作了以下统计表以及统计图.
根据以上信息解答下列问题:
(1)补全扇形图;
(2)题目所给出的线路中,调价后客流量下降百分比最高的线路是 ,调价后里程x(千米)在 范围内的客流量下降最明显.对于表中客流量不降反增而且增长率最高的线路,如果继续按此变化率增长,预计2016年1月这条线路的日均客流量将达到 万人次;(精确到0.1)
(3)小王同学上学时,需要乘坐地铁15.9公里到达学校,每天上下学共乘坐两次.问调价后小王每周(按5天计算)乘坐地铁的费用比调价前多支出 元.(不考虑使用市政一卡通刷卡优惠,调价前每次乘坐地铁票价为2元)
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.
(1)求证:△APB≌△APD;
(2)已知DF∶FA=1∶2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.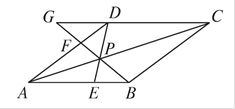
如图所示,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住.为了寻找这只老鼠,猫头鹰向上飞至树顶C处.DF=4米,短墙底部D与树的底部A间的距离为2.7米,猫头鹰从C点观察F点的俯角为53°,老鼠躲藏处M (点M在DE上)距D点3米.
(参考数据:sin 37°≈0.60, cos 37°≈0.80,tan 37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少再要飞多少米(精确到0.1米)?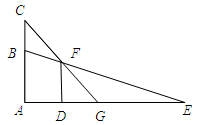
某中学为了落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
某市“每天锻炼一小时,幸福生活一辈子”活动已开展了一年,为了了解该市此项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取200名居民;
B.从一个城镇的不同住宅楼中随机选取200名居民;
C.从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象,然后进行调查.
(1)在上述调查方式中,你认为比较合理的一个是_______(填序号).
(2)由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图,在这个调查中,200名居民每天锻炼2小时的人数是多少?
(3)若该市有100万人,则请你利用(2)中的调查结果,估计该市每天锻炼2小时及以上的人数.
(4)你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.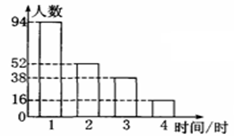
“中国梦”关乎每个人的幸福生活.为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
| 等级 |
成绩(用s表示) |
频数 |
频率 |
| A |
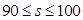 |
x |
0.08 |
| B |
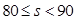 |
35 |
y |
| C |
s<80 |
11 |
0.22 |
| 合计 |
50 |
1 |
请根据上表提供的信息,解答下列问题:
(1)表中x的值为,y的值为;
(2)将本次参赛作品获得A等级的学生依次用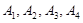 表示,现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树形图或列表法求恰好抽到学生
表示,现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树形图或列表法求恰好抽到学生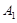 和
和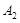 的概率.
的概率.