已知抛物线C1的函数解析式为y=ax2+bx-3a(b<0),若抛物线C1经过点(0,-3),方程ax2+bx-3a=0的两根为x1,x2,且 =4.
=4.
(1)求抛物线C1的顶点坐标.
(2)已知实数x>0,请证明x+ ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+ =2.
=2.
(3)若将抛物线C1先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设A(m,y1),B(n,y2)是C2上的两个不同点,且满足:∠AOB=90°,m>0,n<0.请你用含m的表达式表示出△AOB的面积S,并求出S最小值及S取最小值时直线OA的函数解析式.
某校需刻录一批电脑光盘,若到电脑公司刻录,每张需8元(包括空白光盘费);若学校自己刻录,除租用刻录机需120元外,每张还需成本4元(包括空白光盘费),问刻录这批光盘到电脑公司刻录费用省,还是自己刻录省?请说明理由。
如图,一块长3m、宽1.5m的矩形黑板,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?答:。
如图,已知正比例函数和反比例函数的图象都经过点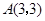 .
.求正比例函数和反比例函数的解析式;
把直线OA向下平移后与反比例函数的图象交于点
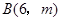 ,求
,求 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;第(2)问中的一次函数的图象与
 轴、
轴、 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积
 与四边形OABD的面积S满足:
与四边形OABD的面积S满足: ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.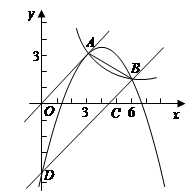
某电视机生产厂家去年销往农村的某品牌电视机每台的售价y(元)与月份x之间满足函数关系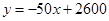 ,去年的月销售量p(万台)与月份x之间成一次函数关系,其中两个月的销售情况如下表:
,去年的月销售量p(万台)与月份x之间成一次函数关系,其中两个月的销售情况如下表:
求该品牌电视机在去年哪个月销往农村的销售金额最大?最大是多少?
)由于受国际金融危机的影响,今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了
 ,且每月的销售量都比去年12月份下降了1.5m%.国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴.受此政策的影响,今年3至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台.若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元,求
,且每月的销售量都比去年12月份下降了1.5m%.国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴.受此政策的影响,今年3至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台.若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元,求 的值(保留一位小数).
的值(保留一位小数).
(参考数据: ,
,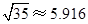 ,
, ,
, )
)
如图,已知:等边三角形 的边长为6,点
的边长为6,点 、
、 分别在边
分别在边 、
、 上,且
上,且 . 点
. 点 从点
从点 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点 运动的时间为
运动的时间为 秒. 当
秒. 当 时,直线
时,直线 与过点
与过点 且平行于
且平行于 的直线相交于点
的直线相交于点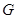 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
, 与
与 相交于点
相交于点
用
 的代数式表示
的代数式表示 ;
;设△
 的面积为
的面积为 ,写出
,写出 与
与 的函数关系式;
的函数关系式;当
 为何值时,点
为何值时,点 和点
和点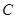 是线段
是线段 的三等分点?
的三等分点?