已知菱形ABCD的边长为1．∠ADC=60°，等边△AEF两边分别交边DC、CB于点E、F。（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点．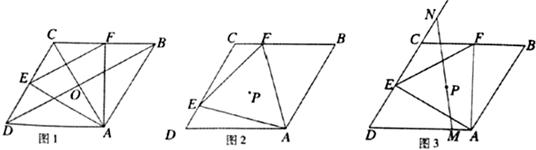
(1)求证：菱形ABCD对角线AC、BD交点O即为等边△AEF的外心；
(2)若点E、F始终分别在边DC、CB上移动．记等边△AEF的外心为点P．
①猜想验证：如图2．猜想△AEF的外心P落在哪一直线上，并加以证明；
②拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，试判断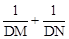
是否为定值．若是．请求出该定值；若不是．请说明理由。
列方程解应用题：
随着人们节能意识的增强，节能产品的销售量逐年增加．某地区高效节能灯的年销售量2009年为10万只，预计2011年将达到14．4万只．求该地区2009年到2011年高效节能灯年销售量的平均增长率．
如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，连接DE．若DE：AC=3：5，则
的值为 ．
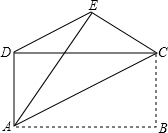
用适当的方法解下列方程：
（1）
（2）
计算
（1）（
－
）0－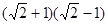
＋
（2）
如图，在平面直角坐标系中，点M是第一象限内一点，过M的直线分别交x轴，y轴的正半轴于A，B两点，且M是AB的中点．以OM为直径的⊙P分别交x轴，y轴于C，D两点，交直线AB于点E（位于点M右下方），连结DE交OM于点K．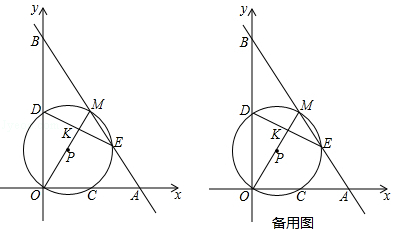
（1）若点M的坐标为（3，4），
①求A，B两点的坐标；
②求ME的长．
（2）若
，求∠OBA的度数．
（3）设tan∠OBA=x（0＜x＜1），
，直接写出y关于x的函数解析式．