(本小题满分14分)
已知几何体 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形. (Ⅰ)求此几何体的体积;
(Ⅰ)求此几何体的体积;
(Ⅱ)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅲ)探究在 上是否存在点Q,使得
上是否存在点Q,使得 ,并说明理由.
,并说明理由.
(本小题满分12分)
四个大小相同的小球分别标有数字1、1、2、2,把它们放在一个盒子里,从中任意摸出两个小球,它们所标有的数字分别为 、
、 ,记
,记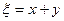 ;
;
(Ⅰ)求随机变量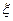 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设“函数 在区间
在区间 上有且只有一个零点”为事件
上有且只有一个零点”为事件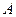 ,求事件
,求事件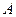 发生的概率.
发生的概率.
(本题满分12分)
已知向量


 ,函数
,函数
 ·
· ,
,
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)如果△ABC的三边a、b、c满足 ,且边b所对的角为
,且边b所对的角为 ,试求
,试求 的范围及函数
的范围及函数 的值域.
的值域.
(本题满分14分)
已知二次函数 的图像过点
的图像过点 ,且
,且 ,
, .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若数列 满足
满足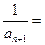
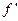
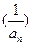 ,且
,且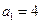 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)记 ,数列
,数列 的前
的前 项和
项和 ,求证:
,求证: .
.
(本题满分14分)
如图,三角形ABC中,AC=BC= ,ABED是边长为1
,ABED是边长为1
的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(Ⅰ)求证:GF//底面ABC;
(Ⅱ)求证:AC⊥平面EBC;
(Ⅲ)求几何体ADEBC的体积V.