如图,在棱长为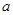 的正方体
的正方体 中,
中, 为
为 的中点,
的中点, 为
为 上任意一点,
上任意一点, 为
为 上任意两点,且
上任意两点,且 的长为定值,则下面的四个值中不为定值的是 ( )
的长为定值,则下面的四个值中不为定值的是 ( )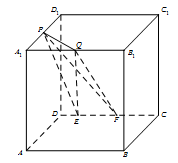
A.点 到平面 到平面 的距离 的距离 |
B.三棱锥 的体积 的体积 |
C.直线 与平面 与平面 所成的角 所成的角 |
D.二面角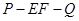 的大小 的大小 |
(本小题满分12分)已知抛物线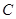 :
: 的焦点为
的焦点为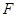 ,若抛物线
,若抛物线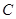 经过圆
经过圆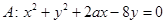 的圆心,且
的圆心,且 .
.
(1)求抛物线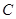 的方程及a的值;
的方程及a的值;
(2)设直线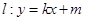 与抛物线
与抛物线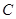 有唯一公共点
有唯一公共点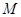 ,且直线
,且直线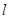 与抛物线的准线交于点
与抛物线的准线交于点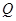 ,试探究,在
,试探究,在
坐标平面内是否存在点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求出点
?若存在,求出点 的坐标,若不存在,
的坐标,若不存在,
说明理由.
(本小题满分12分)如图,在四棱柱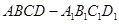 中,底面
中,底面 是等腰梯形,
是等腰梯形, ∥
∥ ,
, ,
, ,顶点
,顶点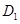 在底面
在底面 内的射影恰为点
内的射影恰为点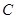 .
.
(1)求证: ;
;
(2)若直线 与直线
与直线 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成角(锐角)的
所成角(锐角)的
余弦函数值.
(本小题满分12分)心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
| 几何题 |
代数题 |
总计 |
|
| 男同学 |
22 |
8 |
30 |
| 女同学 |
8 |
12 |
20 |
| 总计 |
30 |
20 |
50 |
(1)能否据此判断有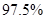 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5~7分钟,乙每次解答一道几何题所用的时
间在6~8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率;
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为 ,求
,求 的分布列及数学期望
的分布列及数学期望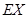 .
.
下面临界值表仅供参考:
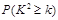 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
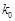 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
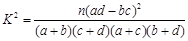 .
.
(本小题满分12分)在△ABC中,内角 所对的边分别为
所对的边分别为 ,若
,若 .
.
(1)求证: 成等比数列且
成等比数列且 ;
;
(2)若 ,求△ABC的面积
,求△ABC的面积 .
.
(本小题满分10分)选修4-5:不等式证明选将
设函数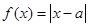
(1) 的解集为R,求实数a的取值范围;
的解集为R,求实数a的取值范围;
(2)若 的解集为
的解集为 ,
, ,求证:
,求证: .
.