阅读下列材料:
解答“已知x-y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:因为x-y=2,所以x=y+2.
因为x>1,所以y+2>1.
因为y<0,所以-1<y<0. ①
同理得1<x<2. ②
有①+ ②得-1+1<x+y<0+2,
所以x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
(1)已知x-y=3,且x>2,y<1,则x+y的取值范围是_____________________。
(2)已知y>1,x<-1,若x-y=a成立,求x+y的取值范围(结果用含a的式子表示)。
(本题12分)△ABC在直角坐标系中的位置如图所示,直线l经过点(-1,0),并且与y轴平行. 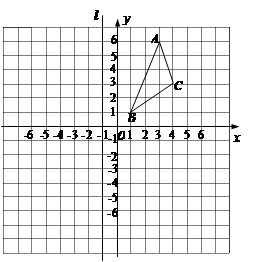
(1)①将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1,在图中画出△A1B1C1;
②求出由点C运动到点C1所经过的路径的长.
(2)①△A2B2C2与△ABC关于直线l对称,画出△A2B2C2,并写出△A2B2C2三个顶点的坐标;
②观察△ABC与△A2B2C2对应点坐标之间的关系,写出直角坐标系中任意一点P(a,b)关于原点O的对称点M的坐标:____ ______.
(本题10分)如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C = 25°,求∠A的度数。
(本题10分)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交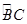 于D.
于D.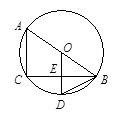
(1)请写出四个不同类型的正确结论;
(2)若BC = 8,ED = 2,求⊙O的半径.
(本题8分)某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
(本题8分)若 是二次函数,求m的值
是二次函数,求m的值