（本小题满分12分）如图， 在直角坐标系xOy中,一次函数y=－
x+m（m为常数）的图像与x轴交于A(-3,0)，与y轴交于点C。以直线x=－1为对称轴的抛物线y=a
+bx+c(a,b,c为常数，且a＞0)经过A，C两点，与x轴正半轴交于点B.
(1)求一次函数及抛物线的函数表达式。
(2)已知在对称轴上是否存在一点P,使得
PBC的周长最小，若存在，请求出点P的坐标.
(3)点D是线段OC上的一个动点（不与点O、点C重合），过点D作DE‖PC交x轴于点E,连接PD、PE。设CD的长为m, △PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值，若存在，请求出最大值：若不存在，请说明理由。
有一句谚语说：“捡了芝麻，丢了西瓜。”意思是说有些人办事只抓一些无关紧要的小事，却忽略了具有重大意义的大事。据测算，5万粒芝麻才200克，你能换算出1粒芝麻有多少克吗？可别“占小便宜吃大亏”噢！（把你的结果用科学记数法表示）
计算与化简
（1） 计算：
（2） 计算：
（3）计算：
（4）计算：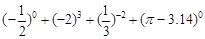
（5）先化简，再求值：
，其中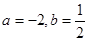
2012年7月6日在湖南省展览馆举行了长沙动漫展，很多中学生也对动漫产生了浓厚
的兴趣，某动漫公司决定在假期举行一次中学生动漫画展，经调查发现，活动最低票价
为10元，如果以10元票价开放，平均每天有100个学生来观看，若票价每提高1元，
则相应减少10个参观者。
（1）写出平均每天观看动漫展的学生人数y（单位：人）与票价x (x为整数，单位：元)之间的关系；
（2）如果要使每天总收入为910元，票价应定为多少元？
如 图，⊙O内切于△ABC，切点分别为D、E、F。已知∠B=50°，∠C=60°，连接D E、D F，求∠EDF。
如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，且∠AED＝45º．
求证：CD是⊙O的切线.