（本小题满分12分）某城市持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一，为此该城市实施了机动车尾号限行政策。现有家报社想调查了解该市区公民对“车辆限行”的态度，在该城市里随机抽查了50人，将调查情况进行整理后制成下表：
| 年龄（岁） |
[15，25） |
[25，35） |
[35，45） |
[45，55） |
[55，65） |
[65，75] |
| 频 数 |
2 |
4 |
20 |
14 |
5 |
5 |
| 支持的人数 |
1 |
3 |
15 |
11 |
4 |
4 |
（Ⅰ）请估计该市公民对“车辆限行”的支持率（答案用百分比表示）；
（Ⅱ）若从年龄在
，
的被调查者中采用分层抽样选取3人进行跟踪调查，求选取的3人中有2人不支持“车辆限行”的概率．
．选修4—4：坐标系与参数方程
椭圆中心在原点，焦点在
轴上。离心率为
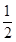，点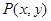
是椭圆上的一个动点，
若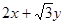
的最大值为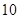
，求椭圆的标准方程．
选修4﹣2：矩阵与变换
已知二阶矩阵
对应的变换将点（﹣2，1）变换成点（0，b），求实数a，b的值．
【选做题】本题包括A，B，C，D四小题，请选定其中两题作答，每小题10分，共计20分，解答时应写出文字说明，证明过程或演算步骤．
A．选修4—1：几何证明选讲
自圆O外一点P引圆的一条切线PA，切点为A，M为PA的中点，
过点M引圆O的割线交该圆于B、C两点，且∠BMP=100°，
∠BPC=40°，求∠MPB的大小．
(本小题满分16分)
已知函数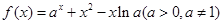
.
（Ⅰ）当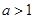
时，求证：函数
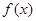在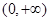
上单调递增；
（Ⅱ）若函数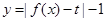
有三个零点，求
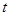的值；
（Ⅲ）若存在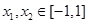
，使得
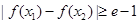，试求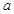
的取值范围.
已知椭圆C：+=1(a＞b＞0)的离心率为，且经过点P(1，)。
(1)求椭圆C的方程；
(2)设F是椭圆C的右焦点，M为椭圆上一点，以M为圆心，MF为半径作圆M。问点M满足什么条件时，圆M与y轴有两个交点?
(3)设圆M与y轴交于D、E两点，求点D、E距离的最大值。