(本小题满分12分)如图,椭圆的右焦点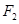 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过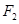 且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且
且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且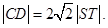

(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P为椭圆上一点,若过点M(2,0)的直线 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足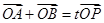 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围.
已知f(x)=1+logx3,g(x)=2logx2,试比较f(x)与g(x)的大小.
2009年春节晚会的现场上无数次响起响亮的掌声,某报记者用仪器测量到最响亮的一次音量达到了90.1分贝.分贝是计量声音强度相对大小的单位.物理学家引入了声压级(spl)来描述声音的大小:把一很小的声压P0=2×10-5帕作为参考声压,把所要测量的声压P与参考声压P0的比值取常用对数后乘以20得到的数值称为声压级.声压级是听力学中最重要的参数之一,单位是分贝(dB).分贝值在60以下为无害区,60—110为过渡区,110以上为有害区.
(1)根据上述材料,列出分贝y与声压P的函数关系式.
(2)某地声压P=0.002帕,试问该地为以上所说的什么区?声音环境是否优良?
已知f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数图象上是否存在不同两点,使过两点的直线平行于x轴?
设函数f(x)=x2-x+b,且f(log2a)=b,log2[f(a)]=2(a≠1),求f(log2x)的最小值及对应的x的值.
设a≠0,对于函数f(x)=log3(ax2-x+a),
(1)若x∈R,求实数a的取值范围;
(2)若f(x)∈R,求实数a的取值范围.