如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A的坐标为(0,2)点B在
抛物线y=ax 2+ax-2上.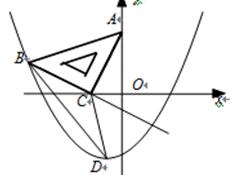
(1)点B的坐标为_____________; 抛物线的关系式为________________________;
(2)若点D是(1)中所求抛物线在第三象限内的一个动点,连接BD、CD.当△BCD的面积最大时,求点D的坐标;
(3)若将三角板ABC沿射线BC平移得到△A ′B ′C′,当C ′ 在抛物线上时.问此时四边形AC C ′A ′是什么特殊四边形?请证明?并判断点A ′是否在抛物线上,请说明理由;
有一道题:“化简求值: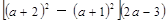 +4a2,其中
+4a2,其中
小毛同学在解题时错误地把“ ”抄成了“
”抄成了“ ”,但显示计算的结果也是正确的,你能解释一下,这是怎么回事吗?
”,但显示计算的结果也是正确的,你能解释一下,这是怎么回事吗?
因式分解: (每题3分)
(1)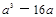 (2)
(2)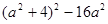
(3) 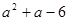 (4)
(4)
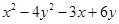
计算: (每题3分)
(1) 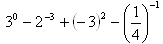 (2)
(2) 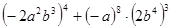
(3)  (4)
(4) 
已知:如图1,在平面直角坐标系中,O为坐标原点,直线y=kx+b与x轴、y轴分别交与点A、B,与双曲线y=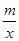 相交于C、D两点,且点D的坐标为(1,6).
相交于C、D两点,且点D的坐标为(1,6).
(1)当点C的横坐标为2时,试求直线AB的解析式,并直接写出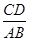 的值为.
的值为.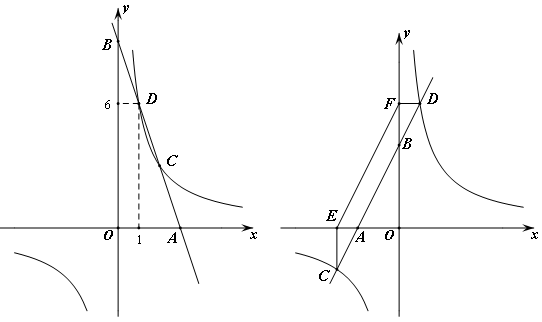
(2)如图2,当点A落在x 轴的负半轴时,过点C作x轴的垂线,垂足为E,过点D作y轴的垂线,垂足为F,连接EF.①判断ΔEFC的面积和ΔEFD的面积是否相等,并说明理由;②当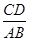 =2时,求tan∠OAB的值.
=2时,求tan∠OAB的值.
某种规格小纸杯的侧面是由一半径为18cm、圆心角是60°的扇形OAB剪去一半径12cm的同心圆扇形OCD所围成的(不计接缝)(如图1).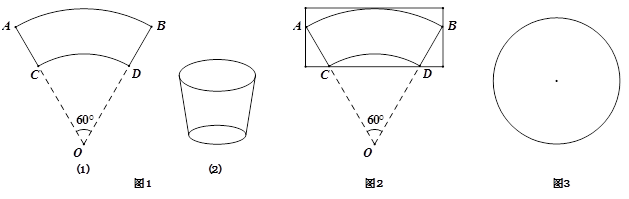
(1)求纸杯的底面半径和侧面积(结果保留π)
(2)要制作这样的纸杯侧面,如果按照图2所示的方式剪裁(不允许有拼接),至少要用多大的矩形纸片
(3)如图3,若在一张半径为18cm的圆形纸片上剪裁这样的纸杯侧面,最多能裁出多少个?