如图（1）（2），在平面直角坐标系中，边长为2的等边△CDE恰好与坐标系中的△OAB重合，现将△CDE绕边AB的中点G（G点也是DE的中点），按顺时针方向旋转180°到△C`DE的位置．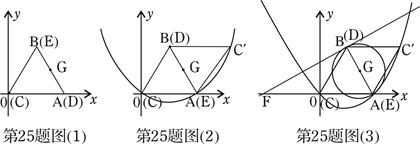 
（1）C`点的坐标为___________；
（2）求经过三点O、A、C` 的抛物线的解析式；
（3）如图（3），⊙G是以AB为直径的圆，过B点作⊙G的切线与x轴相交于点F，求直线BF的解析式；
（4）抛物线上是否存在一点M，使得S△AMF∶S△OAB＝16∶3．若存在，请求出点M的坐标；若不存在，请说明理由．
将对角线分别为5cm和8cm的菱形改为一个面积不变的正方形,则正方形的边长为_______cm．
先化简再求值:当a=9时,求a+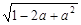
的值,甲乙两人的解答如下:
甲的解答为:原式=a+
=a+(1－a)=1;
乙的解答为:原式=a+=a+(a－1)=2a－1=17． 两种解答中,____的解答是错误的,错误的原因是未能正确地运用二次根次的性质：_______________．
若三角形的三边a、b、c满足a2－4a+4+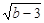
=0,则笫三边c的取值范围是_____________．
一油桶高0.8米，桶内有油，一根木棒长1m，从桶盖小口斜插入桶内，一端到桶底，另一端到小口，抽出木棒，量得棒上浸油部分长0.8m，则桶内油的高度为______。
在坡度为1:2的山坡上种树，要求株距(相邻两树间的水平距离)是6米，斜坡上相邻两树间的坡面距离是________米。