某学校开展“青少年科技创新比赛”活动，“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型．甲、乙两车同时分别从A，B出发，沿轨道到达C处，B在AC上，甲的速度是乙的速度的1．5倍，设t后甲、乙两遥控车与B处的距离分别为d1，d2，则d1，d2与t的函数关系如图，试根据图象解决下列问题：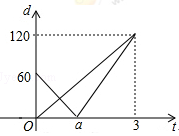
（1）填空：乙的速度v2= 米/分；
（2）写出d1与t的函数关系式；
（3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？
已知一元二次方程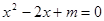
．
（1）若方程有两个实数根，求m的范围；
（2）若方程的两个实数根为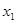
，
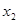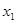，且+3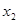=3，求m的值．
先化简：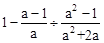
，再选取一个合适的a值代入计算．
（1）计算：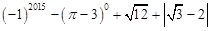
；（2）化简：
．
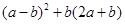在平面直角坐标系中，抛物线C
：y=
x
+4x+4(0＜＜2)，
（1）当C与x轴有唯一交点时，求C的解析式；
（2）若=1，将抛物线C先向右平移2个单位，再向下平移1个单位得抛物线C
，抛物线C与x轴相交于M、N两点（M点在N点的左边），直线y=kx（k＞0）与抛物线C相交于P、Q（P在第三象限）且△NOQ的面积是△MOP的面积的4倍，求k的值；
（3）若A（1，y
），B（0，y
），C（－1，y
）三点均在C上，连BC，作AE∥BC交抛物线C于E，求证：当值变化时，E点在一条直线上．
（本题10分）如图1，梯形ABCD中AB∥CD，且AB=2CD，点P为BD的中点，直线AP交BC于E，交DC的延长线于F．
（1）求证：DC=CF；
（2）求
的值；
（3）如图2，连接DE，若AD⊥ED，求证：
BAE=DBE．