下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| X |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)(参考公式: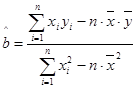 ,
, )
)
已知函数 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(Ⅰ)求ω的值及函数f(x)的单调递增区间;
(Ⅱ)当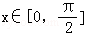 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
已知函数
(Ⅰ)求函数f(x)的定义域
(Ⅱ)若 ,求cosα的值
,求cosα的值
(Ⅲ)在(Ⅱ)条件下,若α是第四象限角,求 的值.
的值.
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=3,直线l的参数方程为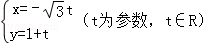 .试在曲线C上求一点M,使它到直线l的距离最大.
.试在曲线C上求一点M,使它到直线l的距离最大.
已知函数f(x)=x2﹣(a+2)x+alnx.
(1)当a=1时,求函数f(x)的极值;
(2)设定义在D上的函数y=g(x)在点P(x0,y0)处的切线方程为l:y=h(x).当x≠x0时,若 >0在D内恒成立,则称P为函数y=g(x)的“转点”.当a=8时,问函数y=f(x)是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=g(x)的“转点”.当a=8时,问函数y=f(x)是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
已知圆O:x2+y2=4和圆C:x2+(y﹣4)2=1.
(Ⅰ)相离;
(Ⅱ)过圆C的圆心C作圆O的切线l,求切线l的方程;
(Ⅲ)过圆C的圆心C作动直线m交圆O于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.