已知函数.
(Ⅰ)求曲线在点处的切线方程;
(Ⅱ)求证:当时,;
(Ⅲ)设实数使得对恒成立,求的最大值.
已知数列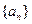 是正数组成的数列,其前n项和
是正数组成的数列,其前n项和 为
为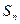 ,对于一切
,对于一切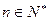 均有
均有 与2的等差中项等于
与2的等差中项等于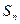 与2的等比中项。
与2的等比中项。
(1)计算 并由此猜想
并由此猜想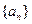 的通项公式
的通项公式 ;
;
(2)用数学归纳法证明(1)中你的猜想。
一次单元测验由20个选择 题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望
题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望
若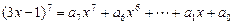 ;
;
求:(1) ;
;
(2)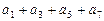 ;
;
(3)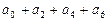 ;
;
在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是 28人,而女乘客晕机为28人,不会晕机的为56 人,
人,
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)试判断是否晕机与性别有关?
甲乙两人各有相同的小球10个,在每人的10个小球 中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。