已知函数.
(Ⅰ)求函数的最小正周期;
(Ⅱ)将函数的图象向右平移个单位长度,再向下平移个单位长度后得到函数的图象,且函数的最大值为2.
(ⅰ)求函数的解析式;
(ⅱ)证明:存在无穷多个互不相同的正整数,使得.
(本小题满分10分)如图:假设三角形数表中的第n+1行的第二个数为 (n≥1,n∈N*)
(n≥1,n∈N*)
(1)归纳出 与
与 的关系式, 并求出
的关系式, 并求出 的通项公式;
的通项公式;
(2)设 ,求证:
,求证: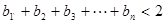
(本小题满分10分)如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器.已知喷水器的喷水区域是半径为5 m的圆.问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?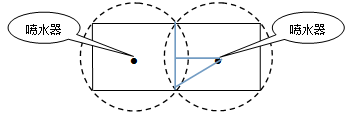
(本小题满分10分)设数列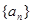 的前n项和为
的前n项和为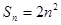 ,
,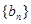 为等比数列,且
为等比数列,且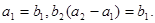
(Ⅰ)求数列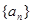 和
和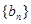 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列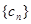 的前n项和Tn.
的前n项和Tn.
(本小题满分10分)已知不等式 .
.
(1)当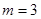 时解此不等式;
时解此不等式;
(2)若对于任意的实数 ,此不等式恒成立,求实数
,此不等式恒成立,求实数 的取值范围。
的取值范围。
(本小题满分14分)已知圆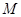 经过第一象限,与
经过第一象限,与 轴相切于点
轴相切于点 ,且圆
,且圆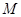 上的点到
上的点到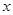 轴的最大距离为2,过点
轴的最大距离为2,过点 作直线
作直线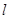 .
.
(1)求圆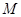 的标准方程;
的标准方程;
(2)当直线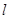 与圆
与圆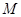 相切时,求直线
相切时,求直线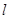 的方程;
的方程;
(3)当直线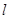 与圆
与圆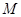 相交于
相交于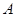 、
、 两点,且满足向量
两点,且满足向量 ,
, 时,求
时,求 的取值范围.
的取值范围.