(本题7分)阅读下列材料:
一般地,n个相同的因数a相乘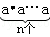 记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算以下各对数的值:
log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式,log24、log216、log264之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN= ;(a>0且a≠1,M>0,N>0)
(4)根据幂的运算法则:an•am=an+m以及对数的含义说明上述结论成立.
(1)解方程: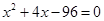 ; (2) 计算:
; (2) 计算: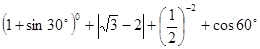
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
玲玲家准备装修一套新住房,若甲、乙两个装饰公司合作,需6周完成,共需装修费为5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.
(1)如果从节约时间的角度考虑,应选哪家公司?
(2)如果从节约开支的角度考虑呢?请说明理由.
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”.
(1)28和2012这两个数是“神秘数”吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?;
(3)两个连续奇数(取正数)的平方差会是“神秘数”吗?为什么?
在解方程组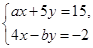 时,由于粗心,甲看错了方程组中的
时,由于粗心,甲看错了方程组中的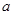 ,得到的解为
,得到的解为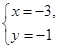 ;乙看错了方程组中的
;乙看错了方程组中的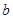 ,得到的解为
,得到的解为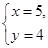 .
.
(1)求原方程组中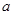 、
、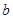 的值各是多少?
的值各是多少?
(2)求出原方程组中的正确解.