如图1,在平面直角坐标系中,已知点A(-6,0),点B(0,8),点C在y轴上,将△OAB沿直线AC对折,使点O落在边AB上的点D处.
(1)求直线AB、AC的解析式.
(2)如图2,过B作BE⊥AC,垂足为E,若F为AB边上一动点,是否存在点F,使C为△EOF内心,若存在,请求出F点坐标,若不存在,请说明理由.
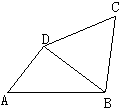
如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD= .求:
.求: 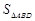 :
: 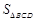 .
.
如图,在菱形ABCD中,AE⊥BC于E,EC=1,sinB=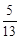 , 求菱形的边长和四边形AECD的周长.
, 求菱形的边长和四边形AECD的周长.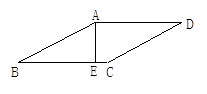
若三角形三边的比是25:24:7,求最小角的正切值、正弦值和余弦值.
在Rt△ABC中,∠C是直角,∠A、∠B、∠C的对边分别是a、b、c,且a=24,c=25,求sinA、cosA、tanA、sinB、cosB、tanB的值.
某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低x元。
(1)填表(不需化简)
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价(元) |
80 |
40 |
|
| 销售量(件) |
200 |
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?