如图①，直线l：y=mx+n（m＜0，n＞0）与x，y轴分别相交于A，B 两点，将△AOB绕点O逆时针旋转90°，得到△COD，
（1）若l：
，E为AD的中点
①在CD上有一动点F ，求当△DEF与△COD相似时点F的坐标；
②如图②，过E作x轴的垂线a，在直线a上是否存在一点Q，使∠CQO=∠CDO？若存在，求出Q点坐标；若不存在，请说明理由
（2）如图③，若l：y=mx﹣4m，G为AB中点，H为CD中点，连接GH，M为GH中点，连接OM．若OM=
，直接写出l的函数解析式．
如图，矩形ABCD中，AB=6，BC=3．点E在线段BA上从B点以每秒1个单位的速度出发向A点运动，F是射线CD上一动点，在点E、F运动的过程中始终保持EF=5，且CF>BE，点P是EF的中点，连接AP．设点E运动时间为ts.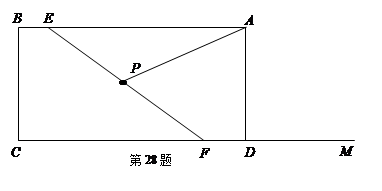
在点E运动过程中，AP的长度是如何变化的？（ ）
| A．一直变短 | B．一直变长 | C．先变长后变短 | D．先变短后变长 |
在点E、F运动的过程中，AP的长度存在一个最小值，当AP的长度取得最小值时，点P的位置应该在．
以P为圆心作⊙P，当⊙P与矩形ABCD三边所在直线都相切时，求出此时t的值，并指出此时⊙P的半径长．
一位数学老师参加本市自来水价格听证会后，编写了一道应用题，题目如下：节约用水、保护水资源，是科学发展观的重要体现.依据这种理念，本市制定了一套节约用水的管理措施，其中规定每月用水量超过
（吨）时，超过部分每吨加收环境保护费
元.下图反映了每月收取的水费
（元）与每月用水量
（吨）之间的函数关系.
请你解答下列问题：将m看作已知量，分别写出当0<x<m和x>m时，
与之间的函数关系式；按上述方案，一家酒店四、五两月用水量及缴费情况如下表所示，那么，这家酒店四、五两月的水费分别是按哪种方案计算的？并求出
的值.
| 月份 |
用水量（吨） |
水费（元） |
| 四月 |
35 |
59.5 |
| 五月 |
80 |
151 |
七年级我们曾学过“两点之间线段最短”的知识，常可利用它来解决两条线段和最小的相关问题，下面是大家非常熟悉的一道习题：
如图1，已知，A，B在直线l的同一侧，在l上求作一点，使得PA+PB最小．
|
|
如图，在△ABD中，∠A=∠B=30°，以AB边上一点O为圆心，过A，D两点作⊙O交AB于C.
判断直线BD与⊙O的位置关系，并说明理由；
连接CD，若CD=5，求AB的长.
已知二次函数
的图象与x轴有且只有一个公共点.求该二次函数的图象的顶点坐标；
若P(n，y1)，Q（n+2，y2）是该二次函数的图象上的两点，且y1＞y2，求实数n的取值范围.