如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.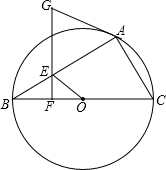
(1)求证:AG与⊙O相切;
(2)若AC=6,AB=8,BE=3,求线段OE的长.
将分别标有数字1,2,3 的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机抽取一张,求抽到奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?恰好是32的概率是多少.
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证: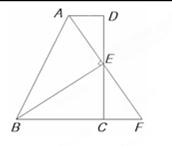
(1)FC=AD;
(2)AB=BC+AD.
如图,△ABC中,BD、CE是△ABC的两条高,点F、M分别是DE、BC的中点. 求证:FM⊥DE.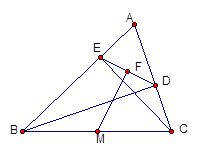
某池塘里养了鱼苗1万条,根据这几年的经验,鱼苗成活率为95%,一段时间后准备打捞出售,第一网捞出40条,称得平均每条鱼重2.5千克,第二网捞出25条,称得平均每条鱼重2.2千克,第三网捞出35条,称得平均每条鱼重2.8千克,试估计这池塘中鱼的质量.
如图,已知正方形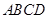 中,点
中,点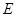 是
是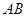 上的一点,连结
上的一点,连结 ,以
,以 为一边,在
为一边,在 的上方作正方形
的上方作正方形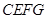 ,连结
,连结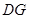 .求证:
.求证: .
.