甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地距离y（km）与时间x（h）之间的函数关系．请根据图象，解答下列问题：
（1）线段CD表示轿车在途中停留了h；
（2）求线段DE对应的函数解析式；
（3）求轿车从甲地出发后经过多长时间追上货车．
（1）计算：
；
（2）化简：（a+b）2+b（a﹣b）．
如图，在平面直角坐标系中，直线
分别交
轴，
轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形．
（1）直接写出点A，B的坐标，并求直线AB与CD交点的坐标；
（2）动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点M从点A出发，沿线段AB以每秒
个单位长度的速度向终点B运动，过点P作
，垂足为H，连接
，
．设点P的运动时间为
秒．
①若△MPH与矩形AOCD重合部分的面积为1，求的值；
②点Q是点B关于点A的对称点，问
是否有最小值，如果有，求出相应的点P的坐标；如果没有，请说明理由．
在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度．
（1）实验操作：在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点的坐标填写在表格中：
（2）观察发现：任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数的图象上；平移2次后在函数的图象上……由此我们知道，平移
次后在函数的图象上．（请填写相应的解析式）
（3）探索运用：点P从点O出发经过次平移后，到达直线
上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．
（1）如图①，在正方形ABCD中，△AEF的顶点E，F分别在BC，CD边上，高AG与正方形的边长相等，求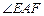
的度数．
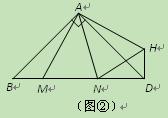
（2）如图②，在Rt△ABD中，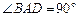
，
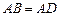，点M，N是BD边上的任意两点，且
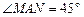，将△ABM绕点A逆时针旋转
至△ADH位置，连接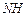
，试判断MN，ND，DH之间的数量关系，并说明理由．
（3）在图①中，连接BD分别交AE，AF于点M，N，若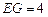
，
，
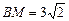，求AG，MN的长．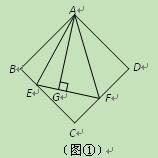
某农机服务站销售一批柴油，平均每天可售出20桶，每桶盈利40元．为了支援我市抗旱救灾，农机服务站决定采取降价措施．经市场调研发现：如果每桶柴油降价1元，农机服务站平均每天可多售出2桶．
（1）假设每桶柴油降价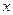
元，每天销售这种柴油所获利润为
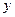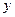元，求与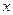之间的函数关系式；
（2）每桶柴油降价多少元后出售，农机服务站每天销售这种柴油可获得最大利润？此时，与降价前比较，每天销售这种柴油可多获利多少元？