如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.
(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31°≈ ,sin31°≈
,sin31°≈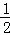 ,tan39°≈
,tan39°≈ ,sin39°≈
,sin39°≈ )
)
因式分解
(1)﹣2a3+12a2﹣18ª
(2)(x2+4)2-16x2
(3)(x2-2x)2+2(x2-2x)+1
计算
(1) (2)(-2x)3-(-x)(3x)2(3)
(2)(-2x)3-(-x)(3x)2(3)
一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.
(1)判断与操作:如图2,矩形ABCD长为5,宽为2,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(2)探究与计算:已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
(3)归纳与拓展:已知矩形ABCD两邻边的长分别为b,c(b<c),且它是4阶奇异矩形,则b:c=___________________________________________(写出所有值).
D、E分别是△ABC的边AB、AC的中点.O是平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、E、F、G.
(1)如图1,当点O在△ABC内时,求证:四边形DEFG是平行四边形;
(2)若点O在△ABC外,其余条件不变,点O的位置应满足什么条件,能使四边形DEFG是菱形?请在画2中补全图形,并说明理由.
如图,直线l与坐标轴分别交于A、B两点,∠BAO=45°,点A坐标为(8,0).动点P从点O出发,沿折线段OBA运动,到点A停止;同时动点Q也从点O出发,沿线段OA运动,到点A停止;它们的运动速度均为每秒1个单位长度.
(1)求直线AB的函数关系式;
(2)若点A、B、O与平面内点E组成的图形是平行四边形,请直接写出点E的坐标;
(3)在运动过程中,当P、Q的距离为2时,求点P的坐标.