(本小题满分13分)已知函数 ,方程
,方程 在
在 上的解按从小到大的顺序排成数列
上的解按从小到大的顺序排成数列
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 的表达式.
的表达式.
求下面数列的前n项和:
1 ,3
,3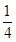 ,5
,5 ,7
,7 ,…
,…
已知数列{an}的首项a1=2a+1(a是常数,且a≠-1),
an=2an-1+n2-4n+2(n≥2),数列{bn}的首项b1=a,
bn=an+n2(n≥2).
(1)证明:{bn}从第2项起是以2为公比的等比数列;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;
(3)当a>0时,求数列{an}的最小项.
已知数列{an}的前n项和为Sn,a1=1,Sn+1=4an+1,设bn=an+1-2an.证明:数列{bn}是等比数列.
等比数列{an}的前n项和为Sn,已知a1+an=66,a2an-1=128,Sn=126,求n和公比q的值.
已知数列{an}的前n项和Sn=2n2+2n,数列{bn}的前n项和Tn=2-bn.
(1)求数列{an}与{bn}的通项公式;
(2)设cn= ·bn,证明:当且仅当n≥3时,cn+1<cn..
·bn,证明:当且仅当n≥3时,cn+1<cn..